こんにちは。東久留米市の学習塾塾長です。
天気予報は曇り時々晴れなのですが、朝から雲が多く晴れ間は見られません。明日も同じような天気になるようで、GW後半はぱっとしない天気が多くなるようです。
平成27年度の開成高校の入試問題に、

を因数分解せよ、という問題がありました。
問題自体は何と言うこともないもので、定石通り、次数の低いyで整理すれば、
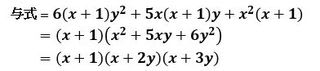 (1)
(1)
と因数分解できます。
また、与式が次式のように因数分解できたとして、
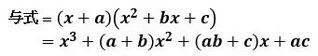 (2)
(2)
と置き、展開、整理し、係数を比較する方法もあります。
ここで、与式と(2)の係数を比較して、
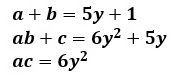 (3)
(3)
とし、3式からyを消去して、整理すると、
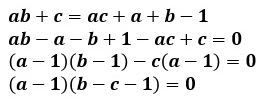
になります。
ここから、a=1で、これを(3)に代入すると、

で、これらを(2)に代入すると、(1)の2行目の式を導くことができます。
さらに、3次方程式の解と係数の関係を使ったり(これは2つ目の方法と似た形になります)、因数定理でx=-1を見つけたりする方法もあります。
また、3次方程式の解の公式を使うのも面白そうです。先ほど少し計算したのですが、上手くいきませんでした。今晩にでも再挑戦します。興味のある人は計算してみてください。
天気予報は曇り時々晴れなのですが、朝から雲が多く晴れ間は見られません。明日も同じような天気になるようで、GW後半はぱっとしない天気が多くなるようです。
平成27年度の開成高校の入試問題に、

を因数分解せよ、という問題がありました。
問題自体は何と言うこともないもので、定石通り、次数の低いyで整理すれば、
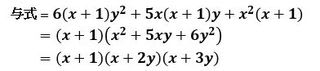 (1)
(1)と因数分解できます。
また、与式が次式のように因数分解できたとして、
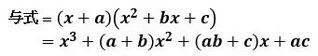 (2)
(2)と置き、展開、整理し、係数を比較する方法もあります。
ここで、与式と(2)の係数を比較して、
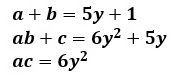 (3)
(3)とし、3式からyを消去して、整理すると、
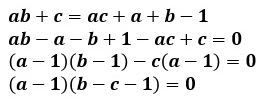
になります。
ここから、a=1で、これを(3)に代入すると、

で、これらを(2)に代入すると、(1)の2行目の式を導くことができます。
さらに、3次方程式の解と係数の関係を使ったり(これは2つ目の方法と似た形になります)、因数定理でx=-1を見つけたりする方法もあります。
また、3次方程式の解の公式を使うのも面白そうです。先ほど少し計算したのですが、上手くいきませんでした。今晩にでも再挑戦します。興味のある人は計算してみてください。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます