こんにちは。東久留米市の学習塾塾長です。
予報では、曇りのち、雨となっていましたが、今は晴れています。風が強いのでこれから曇って雨が降るのかもしれません。
中3の数学では、因数分解を勉強している頃ですが、塾生が因数分解の計算スピードを速くしたいとの希望がありました。
計算スピードを上げる効果的な方法は、ちょっとしたテクニックとたくさんの演習なので、早速、学研のシステムから演習問題をDLしました。この学研システムは演習問題が4段階の難易度に区別してあって、それらをすべてプリントしたのですが、最難度のものは、塾生のリクエストに合わないので使わずに置いておき、パズル好きの私には面白そうだったので、自宅で解いてみました。
出題の出展は、ラ・サール、慶応志木、早稲田実業など難関私立高校で、学校のワークなどにある問題とはレベルが違うのですが、とは言っても、それほど難しくするわけにはいかないようで、図1に示す基本的な因数分解を組み合わせたものがほとんどでした。
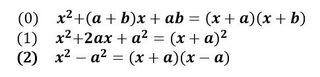
▲図1.因数分解の基本
そこで、図2に示した慶応志木(i)と東大寺学園(ii)で出題された問題を調べてみましょう。
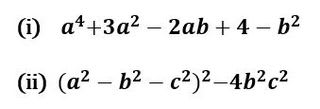
▲図2.難しい因数分解の出題例
(i)の問題は、aの4乗、2乗、bの2乗、abの項などから、aの2乗を最高次にもつ多項式の2乗と、bを最高次にもつ多項式の2乗の差、つまり、それらの和と差の積(図1の(2)の形)となる雰囲気を感じるわけです。
そこで、
与式=a^4+4a^2+4-(a^2+2ab+b^2)
=(a^2+2)^2-(a+b)^2
=(a^2+a+b+2)(a^2-a-b+2)
と、図1の(1)を使ってから(2)を適応して一件落着です。
次に、(ii)ですが、既に和と差の積の形になっているので、
与式=(a^2-b^2-c^2+2bc)(a^2-b^2-c^2-2bc)
までは簡単です。
さらに、
a^2-b^2-c^2+2bc=a^2-(b^2-2bc+c^2)
=a^2-(b-c)^2
=(a+b-c)(a-b+c)
a^2-b^2-c^2-2bc=a^2-(b^2+2bc+c^2)
=a^2-(b+c)^2
=(a+b+c)(a-b-c)
から、答えは、
(a+b+c)(a+b-c)(a-b+c)(a-b-c)
となり、これは、図1の(2)を使って、次に(1)を使い、さらに(2)を適用してお仕舞いです。
これらの例題から判るように、難関高校入試で出題される因数分解は、因数分解の基本形を組み合わせたものになっているので、基本形の因数分解が素早くできるように演習した後に取り組めば、容易に対応できるようになるでしょう。
予報では、曇りのち、雨となっていましたが、今は晴れています。風が強いのでこれから曇って雨が降るのかもしれません。
中3の数学では、因数分解を勉強している頃ですが、塾生が因数分解の計算スピードを速くしたいとの希望がありました。
計算スピードを上げる効果的な方法は、ちょっとしたテクニックとたくさんの演習なので、早速、学研のシステムから演習問題をDLしました。この学研システムは演習問題が4段階の難易度に区別してあって、それらをすべてプリントしたのですが、最難度のものは、塾生のリクエストに合わないので使わずに置いておき、パズル好きの私には面白そうだったので、自宅で解いてみました。
出題の出展は、ラ・サール、慶応志木、早稲田実業など難関私立高校で、学校のワークなどにある問題とはレベルが違うのですが、とは言っても、それほど難しくするわけにはいかないようで、図1に示す基本的な因数分解を組み合わせたものがほとんどでした。
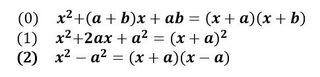
▲図1.因数分解の基本
そこで、図2に示した慶応志木(i)と東大寺学園(ii)で出題された問題を調べてみましょう。
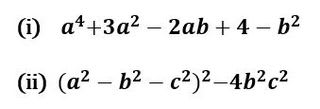
▲図2.難しい因数分解の出題例
(i)の問題は、aの4乗、2乗、bの2乗、abの項などから、aの2乗を最高次にもつ多項式の2乗と、bを最高次にもつ多項式の2乗の差、つまり、それらの和と差の積(図1の(2)の形)となる雰囲気を感じるわけです。
そこで、
与式=a^4+4a^2+4-(a^2+2ab+b^2)
=(a^2+2)^2-(a+b)^2
=(a^2+a+b+2)(a^2-a-b+2)
と、図1の(1)を使ってから(2)を適応して一件落着です。
次に、(ii)ですが、既に和と差の積の形になっているので、
与式=(a^2-b^2-c^2+2bc)(a^2-b^2-c^2-2bc)
までは簡単です。
さらに、
a^2-b^2-c^2+2bc=a^2-(b^2-2bc+c^2)
=a^2-(b-c)^2
=(a+b-c)(a-b+c)
a^2-b^2-c^2-2bc=a^2-(b^2+2bc+c^2)
=a^2-(b+c)^2
=(a+b+c)(a-b-c)
から、答えは、
(a+b+c)(a+b-c)(a-b+c)(a-b-c)
となり、これは、図1の(2)を使って、次に(1)を使い、さらに(2)を適用してお仕舞いです。
これらの例題から判るように、難関高校入試で出題される因数分解は、因数分解の基本形を組み合わせたものになっているので、基本形の因数分解が素早くできるように演習した後に取り組めば、容易に対応できるようになるでしょう。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます