こんにちは。東久留米市の学習塾塾長です。
今回は、2018年のジュニア数学オリンピック予選に出題された面積の問題を取り上げます。
問題は、
「正三角形ABCを、図のように、3辺に平行な線分を1本ずつ引いて分割した。書かれている数は、分割してできた正三角形の面積を表している。このとき、正三角形ABCの面積を求めよ。」
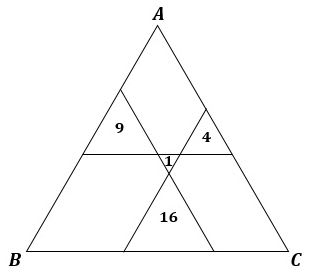
▲問題図
です。
下の図のように、正三角形の辺とそれに平行な線分の交点を、D、E、F、G、P、Qとすると、線分DP、PQ、QGの長さの比は、それらを1辺とする正三角形の面積の平方根の比になるので、 DP:PQ:QG=3:1:2 になります。
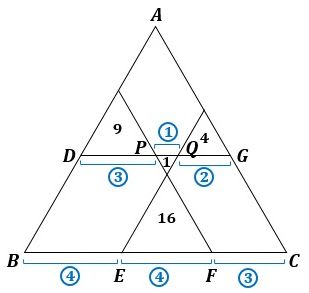
▲図. DP:PQ:QG=3:1:2です
ここで、四角形BEQDと四角形CFPGは平行四辺形なので、BE=DQ、FC=PGから、
BE:FC=4:3 です。
さらに、線分EFは面積16の正三角形の辺なので、
BE:EF:FC=4:4:3
になり、辺BCの長さの比は、4+4+3=11 です。
したがって、正三角形ABCの面積は11×11=121 で、これが答えです。
簡単な問題です。
今回は、2018年のジュニア数学オリンピック予選に出題された面積の問題を取り上げます。
問題は、
「正三角形ABCを、図のように、3辺に平行な線分を1本ずつ引いて分割した。書かれている数は、分割してできた正三角形の面積を表している。このとき、正三角形ABCの面積を求めよ。」

▲問題図
です。
下の図のように、正三角形の辺とそれに平行な線分の交点を、D、E、F、G、P、Qとすると、線分DP、PQ、QGの長さの比は、それらを1辺とする正三角形の面積の平方根の比になるので、 DP:PQ:QG=3:1:2 になります。

▲図. DP:PQ:QG=3:1:2です
ここで、四角形BEQDと四角形CFPGは平行四辺形なので、BE=DQ、FC=PGから、
BE:FC=4:3 です。
さらに、線分EFは面積16の正三角形の辺なので、
BE:EF:FC=4:4:3
になり、辺BCの長さの比は、4+4+3=11 です。
したがって、正三角形ABCの面積は11×11=121 で、これが答えです。
簡単な問題です。





















なので、面積比から1辺が11の正三角形の面積は121√3/4
筆者は面積比が1:121であるため、1辺が1の正三角形の面積は1と書いてあるが、面積比はあくまで2つの図形の面積の比を表すものであり、面積を表すものではない
筆者は勘違いしていると思われる
>1辺が1の正三角形の面積
確かにおっしゃるとおりなのですが、
題意では、図中の数値は「辺長」ではなく「面積」です。
そのため、解説でも面積比から辺比にしっかりと直しておられます。
気になってしまったのでコメントしました。
ご確認ください。
本当ですね、勘違いしていたの私でした。すみません
以後、問題文をしっかり読もうと思います