こんにちは。東久留米市の学習塾塾長です。
道端には雪が積み上げられていますが、道に雪はなく歩きやすくなりました。しかし、また週末に降雪かもしれないと言っていました。
さて、麻布中の算数入試問題ですが、今日は大問6の図形問題です。4つの小問からなり、前半の(1)、(2)は後半のヒントになっています。
問題は、「正三角形を敷き詰めた平面上で、(1)図1の線分XYを点Yを中心にして反時計回りに60°回転させたときの点Zを図に書き入れなさい。(2)角XOZの大きさは何度でしょう」というものです。

▲図1.麻布中算数入試問題大問6(1)(2)
これは簡単で、平面上に敷き詰めた正三角形の頂点を格子点としてみなして、点Xと点Yまでの長さが線分XYの長さと同じになる点を見つければOKです。すると、△XYZは正三角形になるので、∠XYZ=60°となり、線分XYを点Yを中心に60°回転させたことになります。(2)は、二等辺三角形の頂点と底辺の中点とを結んだ直線は、底辺と直交するので、90°になります。
次に、小問(3)です。問題は、「図2にある正六角形ABCDEFのBDとCFとの交点をIとし、点Aと点Iとを重ねて折り目をつけます。そのとき、折り目が辺EFと辺ABと交わった点をそれぞれ点Pと点Qとした場合、EP:PF、AB:QBの比を求めよ」というものです。

▲図2.麻布中算数入試問題大問6(3)
これは、前半のヒントがないと難しいです。そこで、正六角形ABCDEF内に、それらの頂点と格子点が一致するように、正三角形を敷き詰めてみると図3のようになります。これは小問(1)と同じになり、簡単になりました。ポイントは、点Iも敷き詰めた正三角形の格子点になるということです。
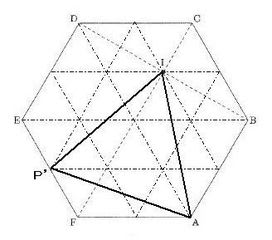
▲図3.麻布中算数入試問題大問6(3)説明図(1)
そこで、平面を隙間なく敷き詰めることができる正多角形として、正三角形以外に正方形と正六角形があるので、正方形で敷き詰めてみます。

▲図4.麻布中算数入試問題大問6(3)説明図(2)
図4で判るように正方形で敷き詰め場合も、点Iは格子点に一致しました。つまり、正方形を敷き詰めても解けるということです。さらに、敷き詰める図形は正多角形でなくても良く、長方形、菱型、平行四辺形でもOKです。繰り返しますが、ポイントは、各頂点が格子点となるように図形を敷き詰めたとき、点Iが格子点と一致することです。
このように小問(1)、(2)をヒントにすると易しく解けるのですが、ヒントを使わずに挑戦してみます。
当然、解析的幾何を使えば簡単ですが、これは、図4のように正方形を敷き詰めた座標系を利用することと同じです。そこで一般的な解き方(?)を示します。
方針は、EFの中点をP’として、これがPと一致することを示します。
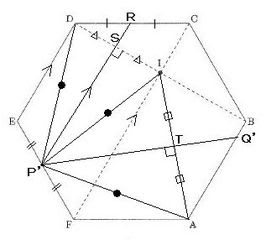
▲図5.麻布中算数入試問題大問6(3)説明図(3)
CDの中点をRとすると、BD⊥P’R、DS=ISなのでP’D=P’I。
また、P’D=P’Aなので、P’I=P’A。つまり、△P’AIは二等辺三角形で、AIの中点SとP’を結んだP’SはAIと直交する。つまり、P’Sは点Aを折り返して点Iに重ねてできる折り目となる。従って、P’とPは一致する。
つまり、PはEFの中点である。Q.E.D.
3回に渡り麻布中の問題を見てきましたが、中学高校数学に繋がる正統派の問題が多いという感じです。御三家と言われるだけのことはありますね。
道端には雪が積み上げられていますが、道に雪はなく歩きやすくなりました。しかし、また週末に降雪かもしれないと言っていました。
さて、麻布中の算数入試問題ですが、今日は大問6の図形問題です。4つの小問からなり、前半の(1)、(2)は後半のヒントになっています。
問題は、「正三角形を敷き詰めた平面上で、(1)図1の線分XYを点Yを中心にして反時計回りに60°回転させたときの点Zを図に書き入れなさい。(2)角XOZの大きさは何度でしょう」というものです。

▲図1.麻布中算数入試問題大問6(1)(2)
これは簡単で、平面上に敷き詰めた正三角形の頂点を格子点としてみなして、点Xと点Yまでの長さが線分XYの長さと同じになる点を見つければOKです。すると、△XYZは正三角形になるので、∠XYZ=60°となり、線分XYを点Yを中心に60°回転させたことになります。(2)は、二等辺三角形の頂点と底辺の中点とを結んだ直線は、底辺と直交するので、90°になります。
次に、小問(3)です。問題は、「図2にある正六角形ABCDEFのBDとCFとの交点をIとし、点Aと点Iとを重ねて折り目をつけます。そのとき、折り目が辺EFと辺ABと交わった点をそれぞれ点Pと点Qとした場合、EP:PF、AB:QBの比を求めよ」というものです。

▲図2.麻布中算数入試問題大問6(3)
これは、前半のヒントがないと難しいです。そこで、正六角形ABCDEF内に、それらの頂点と格子点が一致するように、正三角形を敷き詰めてみると図3のようになります。これは小問(1)と同じになり、簡単になりました。ポイントは、点Iも敷き詰めた正三角形の格子点になるということです。

▲図3.麻布中算数入試問題大問6(3)説明図(1)
そこで、平面を隙間なく敷き詰めることができる正多角形として、正三角形以外に正方形と正六角形があるので、正方形で敷き詰めてみます。

▲図4.麻布中算数入試問題大問6(3)説明図(2)
図4で判るように正方形で敷き詰め場合も、点Iは格子点に一致しました。つまり、正方形を敷き詰めても解けるということです。さらに、敷き詰める図形は正多角形でなくても良く、長方形、菱型、平行四辺形でもOKです。繰り返しますが、ポイントは、各頂点が格子点となるように図形を敷き詰めたとき、点Iが格子点と一致することです。
このように小問(1)、(2)をヒントにすると易しく解けるのですが、ヒントを使わずに挑戦してみます。
当然、解析的幾何を使えば簡単ですが、これは、図4のように正方形を敷き詰めた座標系を利用することと同じです。そこで一般的な解き方(?)を示します。
方針は、EFの中点をP’として、これがPと一致することを示します。

▲図5.麻布中算数入試問題大問6(3)説明図(3)
CDの中点をRとすると、BD⊥P’R、DS=ISなのでP’D=P’I。
また、P’D=P’Aなので、P’I=P’A。つまり、△P’AIは二等辺三角形で、AIの中点SとP’を結んだP’SはAIと直交する。つまり、P’Sは点Aを折り返して点Iに重ねてできる折り目となる。従って、P’とPは一致する。
つまり、PはEFの中点である。Q.E.D.
3回に渡り麻布中の問題を見てきましたが、中学高校数学に繋がる正統派の問題が多いという感じです。御三家と言われるだけのことはありますね。










