面積迷路で数学３

　面積迷路第１集１００番の問題。


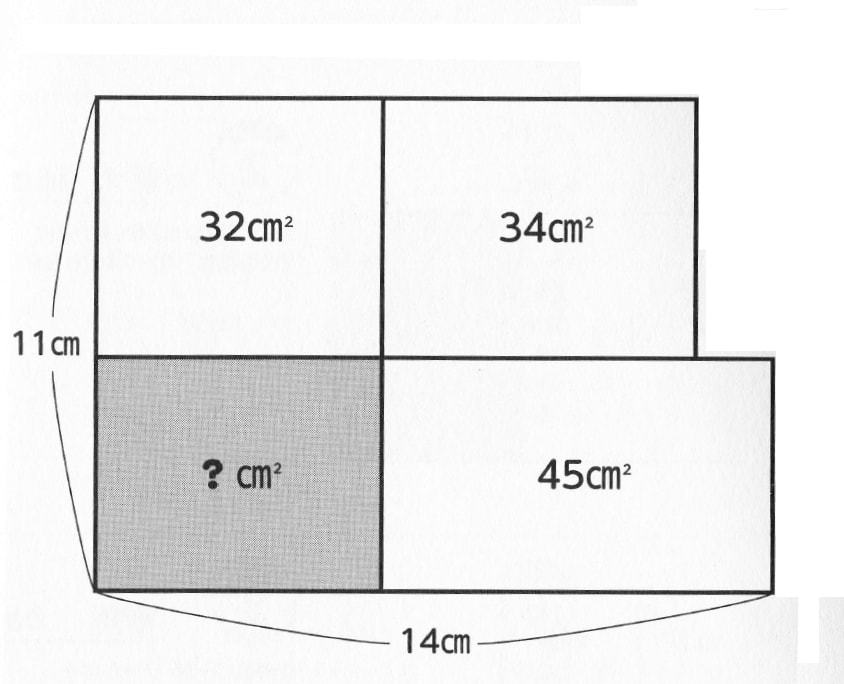
　これを小学校の算数で解くのは難しかった。解答を見たらなんと「禁じ手」を使っていた。
図形についての性質を知らないと解けないのだ。

こんな性質。

============================================================
「長方形を縦横に垂直な線で区切ったときできる４領域について、４領域のうち２領域の面積の合計が
その長方形全体の面積の半分であれば、縦横どちらかの直線は長方形の中心を通る。」
============================================================

　解答をみて私なりに解釈をして文言を工夫してみたらこうなった。
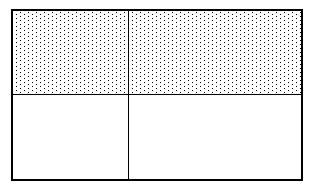
例として、この影をつけた２領域の面積の合計を示す。

この場合は明らかに横の線が長方形の中心を通っていることが分かる。


この問題の場合は左上と右下に影の部分が。


この性質を使うと


上の図で、32＋45＝77、　　11×15＝154 訂正！ 11×14=154 です。(2016.12.14)
154÷2＝77　となっているので、この条件に当てはまる。

したがって、問題図の横の線はこの長方形の中心を通る。
　
左下の？の面積はその上の面積と同じ。

よって答えは　３２平方cm　

では
============================================================
「長方形を縦横に垂直な線で区切ったときできる４領域について、４領域のうち２領域の面積の合計が
その長方形全体の面積の半分であれば、縦横どちらかの直線は長方形の中心を通る。」
============================================================
この性質は小学校の算数を使って、どうやって確かめたら良いのだろうか？

こちらは明らかだが・・・。


この場合はどうなのだろうか

これについて算数の範囲で説明しよう。


つづく

面積迷路で数学２

　面積迷路第１集１００番の問題。


中学校の数学で何とか解いてみよう。
求める？の面積を文字xで表す。右上の欠けた部分を補って、全体を長方形
にし、右上の影の部分の面積をy平方cmとする。


長方形の上側に着目し
左側の面積は　32
右側は　34+y

左の面積と右の面積の比は　下側の　x:45 に等しいから

32:(34+y) = x:45

これより、
x(34+y)=32×45 ・・・(1)

また、長方形全体の面積は　11×14=154 だから
32+34+y+x+45=154

これより、
x+y=43 ・・・(2)

(2)から　y=43-x を(1)に代入すると

　x(34+43-x)=32×45

x(77-x)=32×45

32+45=77 に　注意して32×45はそのままにして式を整理すると

　77x-x^2-32×45=0 （x^2はxの２乗のことと約束する）
　
　x^2-77x+32×45=0

(x-32)(x-45)=0

したがって、　 x=32, x=45
このとき、この順に　y=11, y=-2
よってx=45,y=-2 は不適であるから

　x=32, y=11

したがって、x=32

答え　３２平方cm

これが中学校の数学を使った解法であるが、
小学校の算数ではどうやって解くのだろうか？

つづく

面積迷路で数学１

　面積迷路第１集の１００番の問題については、特殊な性質を使わないと
算数の知識ではうまく解けない。この問題は中学の数学でも何とか解くことが
できる。色々な解法を考えると面白い。


どうやって解くか？

つづく

小学校の算数で５

============================================================
縦と横に同じ数の球を並べようとしたら8個足らず、
縦、横とも1列ずつ減らすと3個余る時、球は何個あるか、
という問題です

方程式を使えば解けますが、小学生が受ける中学受験の問題です

式は8＋3－1＝10
10÷2＝5 5×5＋3＝28で、最初の式の意味がわかりません。

つるかめとか、いろいろありますが、どの計算にあたりますか？
============================================================

　方程式を使うと、小学校の算数のやり方の式が出て来ることが
ある。しかしこのまま、「縦横n個に並べる」では
8＋3－1＝10
10÷2＝5 5×5＋3＝28
という式は出てこなかった。



そこで問題を次のように逆に考える。
============================================================
縦と横に同じ数の球を並べようとしたら3個余る。
縦、横とも1列増やすと8個足りない。
球は何個あるか、
=======================================================

で、図を使ってやってみよう。

「縦と横に同じ数の球を並べようとしたら3個余る。」

こんな感じ。縦横の列は不明だから、・・・で表しておく。

「縦、横とも1列増やすと8個足りない。」
１列を右と下に増やしてみた。

いま増やすために、余った３個を並べてみた所。

このとき８個足りない。


増やす部分だけの図で考える。
１列増やすと、３個と８個がこのように並ぶはず。


つまりここで８＋３＝１１個が「Lの字」に並ぶことになる。


ここで元の列の縦横に何個並ぶのかを求めるには
１１個から角の１個を引いて２で割れば良い。

１１－１＝１０
１０÷２＝５
ということで、初めに５個が縦横に並んでいたことが分かった。


あとは　５×５＋３＝２８　で球の数は　２８個。


質問を繰り返すと・・・
======================================
式は8＋3－1＝10
10÷2＝5 5×5＋3＝28で、最初の式の意味がわかりません。
======================================

これで解決。

おわり

小学校の算数で４

============================================================
縦と横に同じ数の球を並べようとしたら8個足らず、
縦、横とも1列ずつ減らすと3個余る時、球は何個あるか、
という問題です

方程式を使えば解けますが、小学生が受ける中学受験の問題です

方程式を使えば解けますが、小学生が受ける中学受験の問題です

式は8＋3－1＝10
10÷2＝5 5×5＋3＝28で、最初の式の意味がわかりません。

つるかめとか、いろいろありますが、どの計算にあたりますか？
============================================================

　方程式を使うと、小学校の算数のやり方の式が出て来ることが
ある。しかしこのまま、「縦横n個に並べる」では
8＋3－1＝10
10÷2＝5 5×5＋3＝28
という式は出てこなかった。



そこで問題を次のように逆に考える。
============================================================
縦と横に同じ数の球を並べようとしたら3個余る。
縦、横とも1列増やすと8個足りない。
球は何個あるか、
=======================================================

こうすると、縦横n個に並べるとして、球の個数をnで表すことにする。
「縦と横に同じ数の球を並べようとしたら3個余る」から
球の個数は n^2＋3　　　（n^2はnの２乗のこととここでは約束する）

「縦、横とも1列増やすと8個足りない」から
球の個数は　(n＋1)^2ー8

したがって
(n＋1)^2ー8＝n^2＋3
n^2+2n+1-8=n^3+3
移行するとn^2が消えて

2n＝8+3-1 となり8+3-1が出て来た。

2n＝10
n＝5
したがって球の個数は5×5＋3＝28

これらの式から算数で解く手順を考えられそうだ。

2n＝8+3-1の一つ手前の式は2n＋1＝8+3
ここで左辺の2n＋1は
(n+1)^2-n^2　から計算された。

何か思いつかないだろうか？

つづく