正方形敷き詰め問題－２

　続きです。
これはどう敷き詰めますか？


そしてこれは？


で、一番最初のこれ。



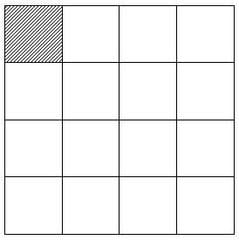
この３種類が皆敷き詰められましたよね。
すると・・・。回転と対称で、４×４の正方形のマス１６個のうちどの箇所を欠損させても必ず敷き詰められることが分かります。
したがって、
定理１　「４×４の正方形はどの１つのマス目を欠損させても、Ｌ字形で敷き詰めることができる」
が成り立ちます。

証明


　一番はじめのタイプはマスの「１」が欠けていますが、回転で「４」、「１６」、「１３」が欠けているものと同じです。
今日のタイプはマスの「２」が欠けていますが、回転で８，１５，９と同じ。
また、対称で３と同じですから、以下回転で１２，１４，５と同じ。
最後のは「６」が欠けていますが、回転で７，１１，１０と同じ。

　以上から１～１６のどれが欠けても、Ｌ字形で敷き詰められます。



では８×８ではどうでしょうか？


４×４の場合、敷きつめ方は１通りですが、これは１通りとはかぎらず、いくつかの解が得られます。（何種類かは調べたことがありません。生徒の課題として良いかも・・・）

楽しい会でした

　東武線谷塚駅交番となりの「とん平」で会があった。秋田から旧知の先生が上京してきたのだ。学校新聞が全国新聞コンクールで今年も入賞したからだ。昨年は千住で飲んだかな？あのあと「靴すり替え事件」があったな。でもブログのおかげで戻ったんでしたね。
　今年は私の退職を祝う会をかねてみなさん集まってくださった。３月３日がまだ先だと思って、前日の２日に飲んで遅くなってしまったので、昨日は途中で帰ることになって申し訳なかった。
　 記念撮影をしたのでアップしておきます。ただし個人情報のためピンぼけの写真です。許諾なくアップしたことをお許し下さい。撮るとき「あれ？フラッシュなくていいの？」と言う人がいましたが、いいのです。そのかわり手ぶれやピンぼけが心配だったので、「もう一度お願いします」と言って２回とってもらいました。１回目がピンぼけと手ぶれ、２回目はまあまあ映っていました。１回目の写真をアップしました。２回目のは後ほどデジカメ写真に出して皆さんに送りたいと思います。昨日はありがとうございました。
　

　十分ピントがぼけているので、知っている人でないと、個人の特定はできないと思いますが、困ると言う方は連絡してください。削除します。
　気楽に参加してしまいました。最後の言葉も何をしゃべったのか余り覚えていませんだめだな～。また、「包んで」行かなかったのが恥ずかしい。仕方がないから今度ね。
　もう一度、皆さんありがとうございました。