図形問題の補助線－平行線－

こんにちは。東久留米市の学習塾塾長です。

予報では最高気温３６°で昨日より暑くなりそうです。中３の塾生はこの暑いなか、毎日頑張っています。

さて、今回は図形問題の補助線についてです。以前に円の中心と円周上の点を結んだ補助線は引いて損なことはないと書きましたが、今回は平行線の補助線です。

まず、図１に平行線の間に２つ線分があり、それらによって成す角の角度を求める問題です。

▲図１．平行線と角の問題

これは中２の数学の教科書に練習問題として取り上げられているほど一般的な問題です。

解法は、図２のように直線ｌとｍに平行で求める角を通る定番の補助線を引きます。すると、直線ｌと３５°を成す角が角度ｘの補助線の上側の角と錯角関係になるので、そこが３５°になり、また同様に、直線ｍと３０°を成す角が角度ｘの補助線の下側の角と錯角関係になるので、そこが３０°になり、結局ｘ＝３５＋３０＝６５°が正解になります。

▲図２．平行線と角の問題の解答

このように平行線と角の問題では平行線に平行な補助線を引いて、錯角関係の角を作ることにより正解に向かって進むことができます。また、求める角度の角が平行線の外側にあるときにもこの解法パターンを使うことができます。

さらに、図３のような凹四角形の１つの角を求める問題にも力を発揮します。

▲図３．凹四角形の求角問題

図３のような問題では、ＢＤやＡＣに補助線を引き、適当な角をａ、ｂなどと置き、三角形の内角の和が１８０°であることを使う解法が一般的ですが、図４のようにＣとＤを通り、ＡＢに平行な補助線を引くと簡単に解けます。（図４が図２に似ていることから想像できると思います）

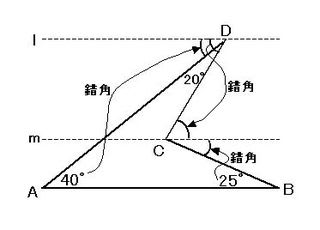
▲図４．凹四角形の求角問題の解答

解答は次の通りで、
∠Ａ＝４０°は、∠ｌＤＡと錯角関係なので、∠ｌＤＡ＝４０°
∠ｌＤＣ＝∠ｌＤＡ＋∠ＡＤＣ＝４０°＋２０°＝６０°
∠ｌＤＣは∠ＤＣｍと錯角関係なので、∠ＤＣｍ＝６０°です。

また、∠ＡＢＣ＝２５°は、∠ＢＣｍと錯角関係なので、∠ＢＣｍ＝２５°

従って、∠ＢＣＤ＝ｘ＝６０°＋２５°＝８５°となります。

以上のように、角度を求める問題では、平行な補助線が力を発揮することが多いので覚えておくとよいでしょう。是非、演習問題などで試してみてください。