ジュニア数学オリンピックの簡単な問題（１０６）

こんにちは。東久留米市の学習塾塾長です。

最低気温が１℃だったので、朝はとても寒かったですが、昼前から少し暖かくなってきました。明日以降も朝晩の冷え込みは厳しくなるようです。体調に気をつけて暖かくして過ごしましょう。

さて、今回は２０１６年ジュニア数学オリンピック予選に出題された最大値の問題を取り上げます。

問題は、
「りんごとみかんが２０１６個ずつあり、これらを次の条件の下で２０１６人に配った：
●すべての果物を配らなければならない。
●果物を１個ももらわない人がいてもよい。
●どの人も２種類合わせて４個までしかもらうことができない。
このとき、りんごをみかんより１個以上多くもらった人は最大で何人存在するか。」
です。

早速、取り掛かりましょう。

りんご１個とみかん０個の人を多くすることで、できるだけりんごの個数を少なくして、りんごをみかんより１個以上多くもらった人を多くすることができます。

仮に、２０１６人全員にりんご１個とみかん０個を配ると、りんごをみかんより１個以上多くもらった人が２０１６人になります。ところが、これでは配らないみかんが２０１６個になり、問題の条件に反してしまいます。

そこで、できるだけ少ない人に２０１６個のみかんを配るとすると、１人に４個のみかんを配ることができるので、その人数は、
２０１６÷４＝５０４（人）
になります。

このとき、図１に示すように、りんご１個とみかん０個の人が１５１２人、りんご０個とみかん４個の人が５０４人で、余ったりんごが５０４個です。

▲図１．りんご１５１２個を１５１２人に、みかん２０１６個を５０４人に配りました

ここから、５０４個の余ったりんごを配りましょう。

図２に示したように、みかん４個を配られた１人から、りんご１個を配られた４人に、みかんを１つずつ配り、さらに余ったりんごからそれらの５人にりんごを１つずつ配ることで、りんごをみかんより１個以上多くもらった人を１人増やすことができます。

つまり、りんご５個で１人増えるということになります。

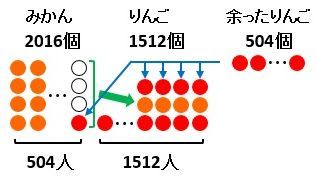
▲図２．りんご５個で、りんごをみかんより１個以上多くもらった人が１人増えます

今、５０４個のりんごが余っているので、
５０４÷５＝１００・・・４
から、この操作によって、りんごをみかんより１個以上多くもらった人が１００人増えることになります。

したがって、りんごをみかんより１個以上多くもらった人の最大値は１５１２＋１００＝１６１２人で、これが答えです。

具体的な配り方の例を、図３に示します。

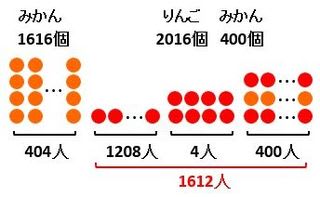
▲図３．配り方の具体例

簡単な問題です。