日本数学オリンピックの簡単な問題（１７）

こんにちは。東久留米市の学習塾塾長です。

太平洋上の高気圧が、西にある梅雨前線を北に押し上げていて、まるで梅雨明けのような状況です。ただ、来週は低気圧が東北地方を横断するのでぱっとしない天気になるようです。

さて、今回は２０１２年日本数学オリンピック予選の図形問題を取り上げます。

問題は、
「三角形ＡＢＣの外心をＯとする。線分ＡＢ上に点Ｄ、線分ＡＣ上に点Ｅをとると、線分ＤＥの中点がＯと一致した。ＡＤ＝８、ＢＤ＝３、ＡＯ＝７のとき、ＣＥを求めよ。ただし、ＸＹで線分ＸＹの長さを表すものとする。」
です。

まず図１のように、問題の図を描きましょう。

▲図１．問題の図を描きました

さらに、Ｏは外心なのでＯＢ＝ＯＣ＝７です。図２に、これらを書き入れましょう。

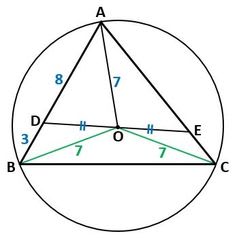
▲図２．Ｏは外心なので、ＯＢ＝ＯＣ＝７です

ここで△ＯＡＢに着目すると、３辺の長さが決まっているので、この三角形についての情報はすべて計算できて、線分ＯＤの長さを求めることができます。

そこで図３のように、Ｏから辺ＡＢに垂線を下ろしその足をＦとすると、△ＯＡＦ、△ＯＤＦは直角三角形になり、それらに三平方の定理を適用します。

▲図３．△ＯＡＦと△ＯＤＦに三平方の定理を適用します

まず、△ＯＡＦでは、
ＯＡ^2＝ＯＦ^2＋ＡＦ^2
です。

ここで、ＯＡ＝７、ＡＦ＝ＡＢ/２＝１１/２ですから、
ＯＦ^2＝７^2－（１１/２）^2
　　　＝４９－１２１/４
　　　＝７５/４
です。

次に、△ＯＤＦでは、
ＯＤ^2＝ＯＦ^2＋ＤＦ^2
です。

ここで、ＯＦ^2＝７５/４、ＤＦ＝１１/２－３＝５/２ですから、
ＯＤ^2＝７５/４＋（５/２）^2
　　　＝７５/４＋２５/４
　　　＝２５
で、
ＯＤ＝５
です。

続いて、△ＯＡＤに着目すると、この三角形も３辺の長さが決まりました。

つまり、図４のように、Ａから辺ＯＤに下ろした垂線の足をＧとすると、ＡＧとＯＧの長さが判るということです。

▲図４．△ＯＡＤに着目し、Ａから辺ＯＤに下ろした垂線の足をＧとします

△ＯＡＧと△ＡＤＧに三平方の定理を適用して、
ＯＡ^2＝ＯＧ^2＋ＡＧ^2　　　　　　　　　　　　　（１）
ＡＤ^2＝ＡＧ^2＋ＤＧ^2　　　　　　　　　　　　　（２）
です。

ＯＡ＝７、ＡＤ＝８、ＤＧ＝ＯＤ－ＯＧ＝５－ＯＧを（１）と（２）に代入して、
７^2＝４９
　　＝ＯＧ^2＋ＡＧ^2　　　　　　　　　　　　　　（３）
８^2＝６４
　　＝ＡＧ^2＋（５－ＯＧ）^2
　　＝ＡＧ^2＋２５－１０ＯＧ＋ＯＧ^2
から
１０ＯＧ＝ＯＧ^2＋ＡＧ^2－３９　　　　　　　　　（４）
です。

ここで（３）を（４）に代入して、
１０ＯＧ＝４９－３９
　　　　＝１０
ＯＧ＝１
です。

これを（３）に代入して、
ＡＧ^2＝４９－１^2
　　　＝４８
ＡＧ＝４√３
です。

次に図５の△ＡＥＧに着目すると、これも直角三角形なので、三平方の定理が適用できます。

▲図５．△ＡＥＧも直角三角形です

つまり、
ＡＥ^2＝ＡＧ^2＋ＥＧ^2
が成り立ちます。

これに、ＡＧ＝４√３、ＥＧ＝ＯＥ＋ＯＧ＝５＋１＝６を代入して、
ＡＥ^2＝４８＋３６
　　　＝８４
ＡＥ＝２√２１
です。

ここまでで、随分と求めたい線分ＣＥに近づいてきました。もう一息です。

さらに、３辺の決まっている三角形を探すと、△ＯＡＥがありました。

これまでと同様、図６のように、Ｏから辺ＡＥに垂線を下ろしその足をＨとします。

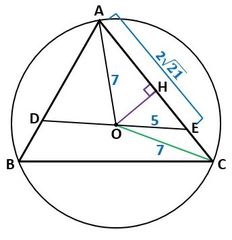
▲図６．△ＯＡＥに着目し、Ｏから辺ＡＥに下ろした垂線の足をＨとします

そこで、△ＯＡＨと△ＯＥＨに三平方の定理を適用して、
ＯＡ^2＝ＯＨ^2＋ＡＨ^2　　　　　　　　　　　　（５）
ＯＥ^2＝ＯＨ^2＋ＥＨ^2　　　　　　　　　　　　（６）
です。

ＯＡ＝７、ＯＥ＝５、ＥＨ＝ＡＥ－ＡＨ＝２√２１－ＡＨを（５）と（６）に代入して、
７^2＝４９
　　＝ＯＨ^2＋ＡＨ^2　　　　　　　　　　　　　（７）
５^2＝２５
　　＝ＯＨ^2＋（２√２１－ＡＨ）^2
　　＝ＯＨ^2＋８４－４√２１ＡＨ＋ＡＨ^2
から
４√２１ＡＨ＝５９＋ＯＨ^2＋ＡＨ^2　　　　　　（８）
です。

ここで、（８）に（７）を代入して、
４√２１ＡＨ＝５９＋４９
　　　　　 ＝１０８
ＡＨ＝２７/√２１
　　＝９√２１/７
です。

最後に、ＡＣ＝２ＡＨからＡＣ＝１８√２１/７で、
ＣＥ＝ＡＣ－ＡＥ
　　＝１８√２１/７－２√２１
　　＝４√２１/７
になり、これが答えです。


合同条件を満たしている三角形では、それに関するすべての情報を求めることができるということ（一般の角（９０°などでない角）については高校で勉強する三角関数が必要です）を頭に入れておくとよいでしょう。また、他の解き方としては、△ＡＢＣの外接円があるので、方べきの定理やトレミーの定理を利用することができそうです。興味のある人は調べてみてください。