中学生でも解ける東大大学院入試問題（７６）

こんにちは。東久留米市の学習塾塾長です。

新年明けましておめでとうございます。今年もよろしくお願い致します。

朝は日差しがあって明るい元旦でしたが、段々雲が多くなってきて、雪も舞い始めました。受験生の皆さんは暖かくして勉強してください。

さて、今回は平成２６年度東大大学院工学系研究科システム創成学の入試問題です。

問題は、
「２ｎ－２本の直線を一筆書きで引いて、等間隔に並んだｎ×ｎ（ｎ＞２）のすべての格子点を通す。
１．ｎ＝３の解を、一筆書きの順路がわかるように示せ。
２．ｎ＝５の解を、一筆書きの順路がわかるように示せ。

ただし、以下の条件を満たすこと。
・格子点を２回以上通ってもよい。
・直線が他の直線と交差してもよい。
・すでに引いてある直線のいかなる区間も上書きしてはいけない。

ｎ＝４のとき、６本の直線ではなく７本の直線で引いた不正解の例を、下図に示す。」

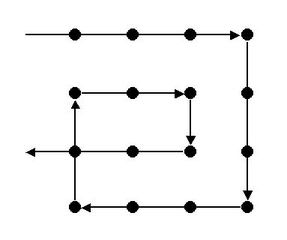
▲不正解の例

▲解答用の点格子（ｎ＝３）

▲解答用の点格子（ｎ＝５）

です。

有名なパズルです。普通に格子点間を結んで一筆書きを完成させようとしても不可能で、一旦格子点でないところから折り返すテクニックを知っていれば簡単な問題です。

ｎ＝３の場合、引くことのできる直線は、２×３－２＝４本です。図１にその解答を示します。格子点を斜めに結ぶのがポイントです。

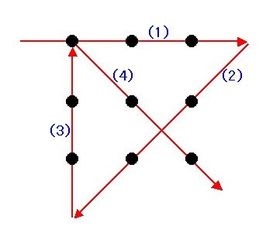
▲図１．ｎ＝３の場合の解答

次に、ｎ＝５の場合ですが、引くことのできる直線は、２×５－２＝１０本となります。ｎ＝３の解答を参考にして考えると、ｎ＝５の場合の最外周の格子点を４本の直線で結んでしまえば（これは簡単で、普通に平行、垂直の直線で結ぶことができます）、残りの３×３の格子点を４本の直線で結んでＯＫとなります。この方針での解答を図２に示します。

▲図２．ｎ＝５の場合の解答（１〈ｎ＝３を参考〉）

他にも図３や４のような解答があります。

▲図３．ｎ＝５の場合の解答（２）

▲図４．ｎ＝５の場合の解答（３）

他にもたくさん解答がありそうです。

このようなパズル問題に限らず、（入試問題など正解のある問題で）正解に素早く辿りつけるか否かは、解法パターン（テクニック）を知っているかどうかに大きく依存します。この解法パターンを身に付けるには多くの演習問題を解いて、どのような解法パターンが使われているのか知ることです。受験生の皆さんは、数多くの演習問題をこなして解法パターンを身に付けましょう。頑張ってください。