ジュニア数学オリンピックの簡単な問題（５１）

こんにちは。東久留米市の学習塾塾長です。

台風一過で、きれいな青空の広がる朝でしたが、瞬く間に雲が増え、その後、明るくなったり、暗くなったりと落ち着かない空模様です。多くの場所で警報や注意報が出ているようなので、気をつけて過ごしましょう。

さて、今回は２０１６年ジュニア数学オリンピック予選に出題された図形問題を取り上げます。

問題は、
「平面上に長さ１０の線分ＡＢがあり、２点Ｐ、Ｑが∠ＡＰＢ＝６０°、∠ＡＱＢ＝１２０°をみたしながらこの平面上を動く。このとき線分ＰＱの長さとしてありうる最大の値を求めよ。」
です。

軌跡の問題です。ある角度が一定値を保って動くときは、円周角を思い起こしましょう。

この問題では、図１のように、ＰとＱは線分ＡＢを弦とする円の周上の点になります。

▲図１．ＰとＱは線分ＡＢを弦とする円の周上にあります

このとき、∠ＡＰＢは∠ＡＱＢの１/２なので、∠ＡＰＢと∠ＡＱＢは円周角と中心角の関係になります。

すると、Ｐがその円周上を動く円の中心Ｏ（Ｏ’）は、Ｑの軌跡上にあり、Ｏ（Ｏ’）は線分ＡＢの垂直二等分線と円Ｏ’（Ｏ）の交点になります。したがって、Ｐ、Ｑの軌跡を含む２つの円の位置関係は、図２のようになります。

▲図２．Ｐ、Ｑの軌跡を含む２つの円の位置関係が判りました

次に、線分ＰＱの長さが最大になる場合を調べてみましょう。

図３のように、Ｏを対称の中心として、ＡとＢがそれぞれ対応する点をＡ’およびＢ’とします。

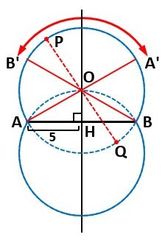
▲図３．ＡとＢの点対称である点をそれぞれＡ’とＢ’とします

ここで、Ｐが劣弧Ａ’Ｂ’上にある場合、線分ＰＱが最大になるのは、ＰとＱがＯについて点対称の位置にあるときで、線分ＰＱの長さは円Ｏの直径の長さと等しくなります。

一方、Ｐが劣弧Ａ’Ｂ’上にない場合、線分ＰＱの長さは円Ｏの直径の長さより小さくなります。

したがって、線分ＰＱの長さの最大値は、円Ｏの直径になります。

あとは、円Ｏの直径を求めればお仕舞いです。

図４のように、線分ＡＢの垂直二等分線とＡＢとの交点をＨとすると、△ＯＡＢは二等辺三角形なので、∠ＡＯＨ＝∠ＢＯＨ＝６０°です。

▲図４．∠ＡＯＨ＝６０°です

つまり、△ＯＡＨは三角定規の片方（内角が３０°、６０°、９０°）と相似で、ＯＡ：ＡＨ＝２：√３が成り立ち、ここではＡＨ＝５なので、ＯＡ＝１０√３/３です。

したがって、円Ｏの直径の長さは１０√３/３×２＝２０√３/３で、これが線分ＰＱの長さとしてありうる最大の値になります。


角度が一定値を保って動く軌跡の問題では、円周角を思い起こせば簡単です。