五角数の問題［桜蔭中］

こんにちは。東久留米市の学習塾塾長です。

今回は、２０１１年桜蔭中入試問題で出題された五角数の問題を取り上げます。

問題は、
「次の［　］にあてはまる数を答えなさい。

　ある数のご石が下の図のような正方形の形に並べられるときに、その数を四角数といいます。はじめの４つの四角数は、１、４、９、１６です。

　１０番目の四角数は［ア］です。
　［イ］番目の四角数は５７６です。

　また、ある数のご石を下の図のような正五角形の形に並べられるときに、その数を五角数といいます。はじめの４つの五角数は、１、５、１２、２２です。

　１０番目の五角数は［ウ］です。
　［エ］番目の五角数は４２５です。」
です。

早速、取り掛かりましょう。

前半の四角数は簡単ですね。

ｎ番目の四角数は ｎ×ｎ ですから、１０番目の四角数は １０×１０＝１００ です。

また、５７６＝２４×２４ から、５７６は２４番目の四角数です。

次に五角数です。

下図のように五角数を分解すると、ｎ番目の五角数は、ｎ－１番目の五角数（●の個数）に●の個数と１個の●を加えた数になります。

ここで図のように、●をグループ分けすると、１つのグループにある●の個数は、正五角形の１辺上に並ぶ碁石の個数より１個少なく、それが３グループあります。

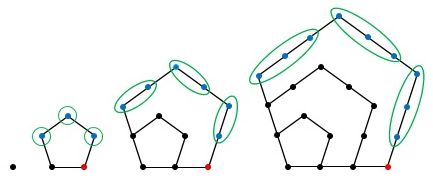
▲図．五角数を分解しました

したがって、ｎ番目の五角数は、
（ｎ番目の五角数）＝（ｎ－１番目の五角数）＋（ｎ－１）×３＋１　　（★）
です。

（★）を使って、順番に計算していくと、
（５番目の五角数）　＝（４番目の五角数）＋（５－１）×３＋１　＝２２＋１２＋１　＝３５
（６番目の五角数）　＝（５番目の五角数）＋（６－１）×３＋１　＝３５＋１５＋１　＝５１
（７番目の五角数）　＝（６番目の五角数）＋（７－１）×３＋１　＝５１＋１８＋１　＝７０
（８番目の五角数）　＝（７番目の五角数）＋（８－１）×３＋１　＝７０＋２１＋１　＝９２
（９番目の五角数）　＝（８番目の五角数）＋（９－１）×３＋１　＝９２＋２４＋１　＝１１７
（１０番目の五角数）＝（９番目の五角数）＋（１０－１）×３＋１＝１１７＋２７＋１＝１４５
になり、１０番目の五角数は１４５です。

１０番目の五角数１４５に３１を加えると１１番目の五角数１７６を求めることができ、さらに、３４、３７、４０・・・を順番に加えていくと、
（１２番目の五角数）＝１７６＋３４＝２１０
（１３番目の五角数）＝２１０＋３７＝２４７
（１４番目の五角数）＝２４７＋４０＝２８７
（１５番目の五角数）＝２８７＋４３＝３３０
（１６番目の五角数）＝３３０＋４６＝３７６
（１７番目の五角数）＝３７６＋４９＝４２５
なので、４２５は１７番目の五角数です。

以上をまとめると、 ア＝１００、イ＝２４、ウ＝１４５、エ＝１７ で、これが答えです。


階差数列を利用して、ｎ番目の五角数の一般項を求めると、
（ｎ番目の五角数）＝ｎ（３ｎ－１）/２
になります。これを使って計算してもＯＫです。