こんにちは。東久留米市の学習塾塾長です。
今回は、2007年開成高入試に出題された作図問題を取り上げます。
問題は、
「△ABCにおいて、AB=6である。このとき、次の問いに答えよ。
(1)∠ACB=60°であるとき、△ABCの外接円における弧ACBの長さを求めよ。
(2)∠ACB=30°、CB≦CAとし、さらに△ABCの面積を6√3とする。このとき、△ABCを作図せよ。
ただし、3点A、B、Cは反時計回りに並ぶものとする。」
です。
まず図1のように、(1)の図を描きましょう。

▲図1.問題(1)の図を描きました
外接円の中心をOとすると、∠AOBと∠ACBは中心角と円周角の関係なので、∠AOB=120°になります。
続いて図2のように、Oから線分ABに垂線を下ろし、その足をHとすると、△AOHは三角定規の直角二等辺三角形でないほうと相似な三角形で、
AO:AH=2:√3
です。
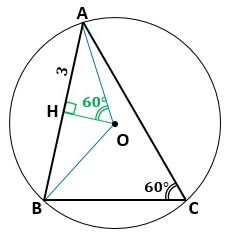
▲図2.Oから線分ABに垂線を下ろしました
ここで、AB=6からAH=3なので、
AO=3×2×1/√3=2√3
です。
したがって、△ABCの外接円の直径は4√3で、その円周の長さは、4√3πです。
弧ACBの長さは、その中心角が240°の扇形の弧の長さですから、
(弧ACBの長さ)=4√3π×2/3=8√3π/3
で、これが答えです。
続いて(2)です。
△ABCの面積が6√3ということは、底辺をABとすると、高さは2√3になり、これは正三角形の一辺と高さの関係を利用すれば作図できそうです。
そこで図3のように、線分ABを一辺とする正三角形を描き、A、Bでない頂点をPとしましょう。

▲図3.線分ABを一辺とする正三角形を描きました
このとき、AB(=PA):PM=2:√3で、AB=6からPM=3√3になります。
さらにPとAからそれぞれ線分ABとPBに垂線を下ろし2本の垂線の交点をGとすると、Gは正三角形PABの重心なので、PG:GM=2:1になり、このとき、PM=3√3から、GM=√3になります。
そこで図4のように、Gを中心として半径がGMの円を描き、その円周と線分PMとの交点でMでないほうをQとすると、QM=2√3になり、Qを通り直線ABに平行な直線Lを引くと、Cは直線L上の点になります。

▲図4.Cは直線L上の点になります
あとは、直線L上にあって、∠ACB=30°、CB≦CAとなるCを見つければOKで、これは円周角が中心角の1/2になることを利用すれば簡単です。
図5のように、Pを中心とし半径PAの円Γを描くと中心角APB=60°から、弧ABに対する円周角は30°になるので、Cは円Γの円周上の点になります。

▲図5.Pを中心とし半径PAの円Γを描くと、弧ABに対する円周角は30°になります
以上から、Cは直線Lと円Γの交点で、かつ、CB≦CAを満たす点になり、したがって、△ABCは図5のようになります。
都立高校の作図問題に比べると少々難しいかもしれません。
今回は、2007年開成高入試に出題された作図問題を取り上げます。
問題は、
「△ABCにおいて、AB=6である。このとき、次の問いに答えよ。
(1)∠ACB=60°であるとき、△ABCの外接円における弧ACBの長さを求めよ。
(2)∠ACB=30°、CB≦CAとし、さらに△ABCの面積を6√3とする。このとき、△ABCを作図せよ。
ただし、3点A、B、Cは反時計回りに並ぶものとする。」
です。
まず図1のように、(1)の図を描きましょう。

▲図1.問題(1)の図を描きました
外接円の中心をOとすると、∠AOBと∠ACBは中心角と円周角の関係なので、∠AOB=120°になります。
続いて図2のように、Oから線分ABに垂線を下ろし、その足をHとすると、△AOHは三角定規の直角二等辺三角形でないほうと相似な三角形で、
AO:AH=2:√3
です。

▲図2.Oから線分ABに垂線を下ろしました
ここで、AB=6からAH=3なので、
AO=3×2×1/√3=2√3
です。
したがって、△ABCの外接円の直径は4√3で、その円周の長さは、4√3πです。
弧ACBの長さは、その中心角が240°の扇形の弧の長さですから、
(弧ACBの長さ)=4√3π×2/3=8√3π/3
で、これが答えです。
続いて(2)です。
△ABCの面積が6√3ということは、底辺をABとすると、高さは2√3になり、これは正三角形の一辺と高さの関係を利用すれば作図できそうです。
そこで図3のように、線分ABを一辺とする正三角形を描き、A、Bでない頂点をPとしましょう。

▲図3.線分ABを一辺とする正三角形を描きました
このとき、AB(=PA):PM=2:√3で、AB=6からPM=3√3になります。
さらにPとAからそれぞれ線分ABとPBに垂線を下ろし2本の垂線の交点をGとすると、Gは正三角形PABの重心なので、PG:GM=2:1になり、このとき、PM=3√3から、GM=√3になります。
そこで図4のように、Gを中心として半径がGMの円を描き、その円周と線分PMとの交点でMでないほうをQとすると、QM=2√3になり、Qを通り直線ABに平行な直線Lを引くと、Cは直線L上の点になります。

▲図4.Cは直線L上の点になります
あとは、直線L上にあって、∠ACB=30°、CB≦CAとなるCを見つければOKで、これは円周角が中心角の1/2になることを利用すれば簡単です。
図5のように、Pを中心とし半径PAの円Γを描くと中心角APB=60°から、弧ABに対する円周角は30°になるので、Cは円Γの円周上の点になります。

▲図5.Pを中心とし半径PAの円Γを描くと、弧ABに対する円周角は30°になります
以上から、Cは直線Lと円Γの交点で、かつ、CB≦CAを満たす点になり、したがって、△ABCは図5のようになります。
都立高校の作図問題に比べると少々難しいかもしれません。










