こんにちは。東久留米市の学習塾塾長です。
秋晴れを楽しみにしていたのですが、いまひとつパッとしない天気です。明日は雨模様ですが、明後日には回復するようなので、秋晴れの日曜日を期待しましょう。
さて、今回は2001年日本数学オリンピック予選に出題された図形問題を取り上げます。
問題は、
「∠ABC=2∠ACBとなる三角形ABCにおいて、∠BACの二等分線と辺BCとの交点をDとする。AB=CDのとき∠BACは何度(°)か。ただし、線分XYの長さをXYで表す。」
です。
早速、図1のように、問題の図を描きましょう。
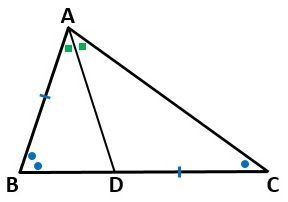
▲図1.問題の図を描きました
AB=CDという条件が離れていて扱い難いので、図2のように、線分CDを上方に平行移動させ平行四辺形ADCFを作りましょう。

▲図2.平行四辺形ADCFを作りました
すると、平行線の錯角は等しいことから、
∠CAE=∠ACD=●
で、平行四辺形の対辺は等しいことから
AD=EC (1)
です。
次に図3のように、BとEを直線で結び、辺ACとの交点をFとし、△ABCと△ECBが合同であることを示します。

▲図3.BとEを直線で結び、辺ACとの交点をFとしました
まず、△ABCの内角の和から
∠ABC(2●)+∠ACB(●)+∠BAC(2■)=3●+2■=180° (2)
です。
一方、△ABEの内角の着目すると、
∠BAE(●+2■)+∠ABE+∠AEB=180°
で、
∠ABE+∠AEB=180°-(●+2■)
です。
すると、(2)から
∠ABE+∠AEB=2●
になります。
ところが、△ABEは二等辺三角形なので、
∠ABE=∠AEB=●
です。
したがって、
∠EBC=∠ABC(2●)-∠ABE(●)
=●
=∠ACD
=∠ACB (3)
です。
また、△FBCと△FAEはどちらも二等辺三角形なので、AF=EF、BF=CFが成り立ちます。
すると、
AC=AF+CF
=EF+BF
=FB (4)
です。
さらに、
BC=CB (5)
で、以上(3)(4)(5)から△ABC≡△ECBです。
したがって、AB=ECで、(1)から
AB=AD
です。
つまり、図4に示すように、△ABDは二等辺三角形で、
∠ABD=∠ADB=2●
になります。

▲図4.∠ABD=∠ADBです
最後に、△ABCと△ABDの内角の和に着目すると、
△ABCから
3●+2■=180°
で、△ABDから
4●+■=180°
が成り立ちます。
この2式から
■=36°
になり、
∠BAC=2■
=2×36°
=72°
で、これが答えです。
他には、図5のように、辺ABをAの方向に延長して二等辺三角形BCGを作るよき方も簡単そうです。興味のある人は調べてみてください。

▲図5.二等辺三角形BCGを作ります
秋晴れを楽しみにしていたのですが、いまひとつパッとしない天気です。明日は雨模様ですが、明後日には回復するようなので、秋晴れの日曜日を期待しましょう。
さて、今回は2001年日本数学オリンピック予選に出題された図形問題を取り上げます。
問題は、
「∠ABC=2∠ACBとなる三角形ABCにおいて、∠BACの二等分線と辺BCとの交点をDとする。AB=CDのとき∠BACは何度(°)か。ただし、線分XYの長さをXYで表す。」
です。
早速、図1のように、問題の図を描きましょう。

▲図1.問題の図を描きました
AB=CDという条件が離れていて扱い難いので、図2のように、線分CDを上方に平行移動させ平行四辺形ADCFを作りましょう。

▲図2.平行四辺形ADCFを作りました
すると、平行線の錯角は等しいことから、
∠CAE=∠ACD=●
で、平行四辺形の対辺は等しいことから
AD=EC (1)
です。
次に図3のように、BとEを直線で結び、辺ACとの交点をFとし、△ABCと△ECBが合同であることを示します。

▲図3.BとEを直線で結び、辺ACとの交点をFとしました
まず、△ABCの内角の和から
∠ABC(2●)+∠ACB(●)+∠BAC(2■)=3●+2■=180° (2)
です。
一方、△ABEの内角の着目すると、
∠BAE(●+2■)+∠ABE+∠AEB=180°
で、
∠ABE+∠AEB=180°-(●+2■)
です。
すると、(2)から
∠ABE+∠AEB=2●
になります。
ところが、△ABEは二等辺三角形なので、
∠ABE=∠AEB=●
です。
したがって、
∠EBC=∠ABC(2●)-∠ABE(●)
=●
=∠ACD
=∠ACB (3)
です。
また、△FBCと△FAEはどちらも二等辺三角形なので、AF=EF、BF=CFが成り立ちます。
すると、
AC=AF+CF
=EF+BF
=FB (4)
です。
さらに、
BC=CB (5)
で、以上(3)(4)(5)から△ABC≡△ECBです。
したがって、AB=ECで、(1)から
AB=AD
です。
つまり、図4に示すように、△ABDは二等辺三角形で、
∠ABD=∠ADB=2●
になります。

▲図4.∠ABD=∠ADBです
最後に、△ABCと△ABDの内角の和に着目すると、
△ABCから
3●+2■=180°
で、△ABDから
4●+■=180°
が成り立ちます。
この2式から
■=36°
になり、
∠BAC=2■
=2×36°
=72°
で、これが答えです。
他には、図5のように、辺ABをAの方向に延長して二等辺三角形BCGを作るよき方も簡単そうです。興味のある人は調べてみてください。

▲図5.二等辺三角形BCGを作ります










