こんにちは。東久留米市の学習塾塾長です。
朝から箱根駅伝をラジオで聴いているのですが、青山学院が往路優勝しそうです。明日の復路が終わると大学センター試験も目前で受験シーズンの到来といった感じです。受験生の皆さん、頑張ってください。
さて、今回は中学受験まで1ヶ月をきったということで、算数の中学入試問題を取り上げます。
問題は、平成27年度桜蔭中のもので、それは、
「下の図1のようなアからケの9個のマスがあります。
このアからケのマスの中に、約数が全部で9個ある整数の約数を小さい順に入れます。たとえば、36の場合は図2のようになります。このとき、次の□にあてはまる数を答えなさい。
(1)アとケとオに書かれている数字の和が241となる整数は□です。
(2)ウとケとキに書かれている数字の積が38416となる整数は□です。」
です。
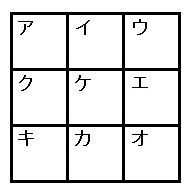
▲図1.問題図(1)
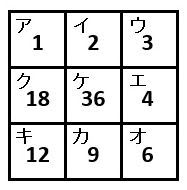
▲図2.問題図(2)
早速(1)から始めましょう。
ここで、ある整数Nの約数の個数が奇数個ということは、Nは平方数になります。
そこで、ケをn^2とすると、オは約数を小さい順に並べたときの真ん中の数なのでnです。(ピンとこないときは下の(2)の解答を参考にしてください)
また、アは1なので、これらから、
ア+ケ+オ=1+n^2+n=241
n^2+n-240=0
(n-15)(n+16)=0
から、
n=15
です。
したがって、
N=15^2=225
となり、これが答えです。
ここでは、2次方程式や因数分解を使っているので、それらを使わないで解きましょう。
まず、ケは241より小さい平方数なので、ケは225(15×15)、196(14×14)、169(13×13)、・・・、4(2×2)、1(1×1)のいずれかになります。
仮に、ケ=225の場合、その約数は小さい順に、1、3、5、9、15、25、45、75、225で、ア=1、オ=15なので、
ア+ケ+オ=1+225+15=241
から、ケは225です。
続いて(2)に進みます。
N(=n^2)の9個の約数を小さい順に、1、p、q、r、s、t、u、v、n^2 とし、これらの9個の約数で、N(=n^2)を割ると、それらは順に、n^2、v、u、t、s、r、q、p、1 となります。
つまり、
n^2=pv=qu=rt=s^2
が成り立ちます。
すると、
ウ×ケ×キ=q・n^2・u
=q・n^2・n^2/q
=n^2・n^2
=n^4
=38416
です。
ここで、38416=(2×7)^4 なので、
n=14
N=14^2=196
で、これが答えになります。
別の方法として、ある整数Nを素因数分解してN=p^a・q^b・r^c・・・と表せるとき、Nの約数の個数が、(a+1)(b+1)(c+1)・・・となることを利用してもよいでしょう。
つまり、
(a+1)(b+1)(c+1)・・・=9
となるので、a=2、b=2、c以下は0 または a=8、b以下は0 です。
・a=2、b=2の場合、N=p^2・q^2 (p<q)で、Nの約数は小さい順に、
1、p、q、p^2、pq、q^2、p^2q、pq^2、(pq)^2
または、
1、p、p^2、q、pq、p^2q、q^2、pq^2、(pq)^2
です。
すると、ウ×ケ×キは、それぞれ
q・(pq)^2・p^2q=(pq)^4
p^2・(pq)^2・q^2=(pq)^4
で、どちらも(pq)^4になります。
したがって、
(pq)^4=38416=(2×7)^4
pq=14
から
N=196
になります。
・a=8の場合、N=p^8 で、Nの約数は小さい順に、
1、p、p^2、p^3、p^4、p^5、p^6、p^7、p^8
です。
すると、ウ×ケ×キは、
p^2・p^6・p8=p^16
で、
p^16=38416=(2×7)^4
を満たす整数pはありません。
38416の素因数分解に手間が掛かりそうですが、女子御三家の桜蔭中を受験する小6生には簡単なのでしょうね。流石です。
朝から箱根駅伝をラジオで聴いているのですが、青山学院が往路優勝しそうです。明日の復路が終わると大学センター試験も目前で受験シーズンの到来といった感じです。受験生の皆さん、頑張ってください。
さて、今回は中学受験まで1ヶ月をきったということで、算数の中学入試問題を取り上げます。
問題は、平成27年度桜蔭中のもので、それは、
「下の図1のようなアからケの9個のマスがあります。
このアからケのマスの中に、約数が全部で9個ある整数の約数を小さい順に入れます。たとえば、36の場合は図2のようになります。このとき、次の□にあてはまる数を答えなさい。
(1)アとケとオに書かれている数字の和が241となる整数は□です。
(2)ウとケとキに書かれている数字の積が38416となる整数は□です。」
です。

▲図1.問題図(1)

▲図2.問題図(2)
早速(1)から始めましょう。
ここで、ある整数Nの約数の個数が奇数個ということは、Nは平方数になります。
そこで、ケをn^2とすると、オは約数を小さい順に並べたときの真ん中の数なのでnです。(ピンとこないときは下の(2)の解答を参考にしてください)
また、アは1なので、これらから、
ア+ケ+オ=1+n^2+n=241
n^2+n-240=0
(n-15)(n+16)=0
から、
n=15
です。
したがって、
N=15^2=225
となり、これが答えです。
ここでは、2次方程式や因数分解を使っているので、それらを使わないで解きましょう。
まず、ケは241より小さい平方数なので、ケは225(15×15)、196(14×14)、169(13×13)、・・・、4(2×2)、1(1×1)のいずれかになります。
仮に、ケ=225の場合、その約数は小さい順に、1、3、5、9、15、25、45、75、225で、ア=1、オ=15なので、
ア+ケ+オ=1+225+15=241
から、ケは225です。
続いて(2)に進みます。
N(=n^2)の9個の約数を小さい順に、1、p、q、r、s、t、u、v、n^2 とし、これらの9個の約数で、N(=n^2)を割ると、それらは順に、n^2、v、u、t、s、r、q、p、1 となります。
つまり、
n^2=pv=qu=rt=s^2
が成り立ちます。
すると、
ウ×ケ×キ=q・n^2・u
=q・n^2・n^2/q
=n^2・n^2
=n^4
=38416
です。
ここで、38416=(2×7)^4 なので、
n=14
N=14^2=196
で、これが答えになります。
別の方法として、ある整数Nを素因数分解してN=p^a・q^b・r^c・・・と表せるとき、Nの約数の個数が、(a+1)(b+1)(c+1)・・・となることを利用してもよいでしょう。
つまり、
(a+1)(b+1)(c+1)・・・=9
となるので、a=2、b=2、c以下は0 または a=8、b以下は0 です。
・a=2、b=2の場合、N=p^2・q^2 (p<q)で、Nの約数は小さい順に、
1、p、q、p^2、pq、q^2、p^2q、pq^2、(pq)^2
または、
1、p、p^2、q、pq、p^2q、q^2、pq^2、(pq)^2
です。
すると、ウ×ケ×キは、それぞれ
q・(pq)^2・p^2q=(pq)^4
p^2・(pq)^2・q^2=(pq)^4
で、どちらも(pq)^4になります。
したがって、
(pq)^4=38416=(2×7)^4
pq=14
から
N=196
になります。
・a=8の場合、N=p^8 で、Nの約数は小さい順に、
1、p、p^2、p^3、p^4、p^5、p^6、p^7、p^8
です。
すると、ウ×ケ×キは、
p^2・p^6・p8=p^16
で、
p^16=38416=(2×7)^4
を満たす整数pはありません。
38416の素因数分解に手間が掛かりそうですが、女子御三家の桜蔭中を受験する小6生には簡単なのでしょうね。流石です。










