本日は、無償の学習塾「あゆむ学習室」の学習指導に参加しました。
中学二年生の生徒さんに、数学の「二元一次方程式の解法」を解説しました。
【二元一次方程式】
(例題)
Aさんの家から駅までの道のりは900mある。Aさんが家から駅に行くとき、2分間走ってから残りの道のりを歩くと10分かかり、3分間走ってから残りの道のりを歩くと9分かかるという。Aさんの走る速さと歩く速さは、それぞれ毎分何mか。
問題文より、歩いた時間を算出できる。
2分間走った場合は、歩いた時間は 10-2=8分
3分間走った場合は、歩いた時間は 9-3=6分
走る速さを毎分xm,歩く速さを毎分ymとおく。以下のように図で考えると良い。

・距離(m)=速さ(毎分〇m)×時間(分)
・歩いた距離+走った距離=家から駅までの道のり
であることに着目し、以下の連立方程式を立てる。
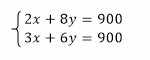
また、方程式は両辺に同じ値を乗じても成立することから、以下のように考えても良い。

これを解くと、
x=150,y=75
従って、走る速さは毎分150m,歩く速さは毎分75mである。
文章題の方程式を解く際は、以下の点を意識して下さい。
1.
状況を把握するために図にまとめる。
2.
方程式の解を求めた後、解を元の式に代入して(左辺)=(右辺)の成立を検証することにより検算できる。
3.
負の値になり得ない事柄(速さや商品の金額など)をxやyでおき、計算すると負の値になってしまった場合は、方程式の立て方が不適切だったり、計算ミスしていることを示している。このとき、これらの見直しが必要である。
計算の進め方は良くできていました。難易度が高めの問題に挑戦して、更なる向上を目指していきたいです。
 あゆむ学習室のサマースクールについては、こちらをご覧下さい。
あゆむ学習室のサマースクールについては、こちらをご覧下さい。
中学二年生の生徒さんに、数学の「二元一次方程式の解法」を解説しました。
【二元一次方程式】
(例題)
Aさんの家から駅までの道のりは900mある。Aさんが家から駅に行くとき、2分間走ってから残りの道のりを歩くと10分かかり、3分間走ってから残りの道のりを歩くと9分かかるという。Aさんの走る速さと歩く速さは、それぞれ毎分何mか。
問題文より、歩いた時間を算出できる。
2分間走った場合は、歩いた時間は 10-2=8分
3分間走った場合は、歩いた時間は 9-3=6分
走る速さを毎分xm,歩く速さを毎分ymとおく。以下のように図で考えると良い。

・距離(m)=速さ(毎分〇m)×時間(分)
・歩いた距離+走った距離=家から駅までの道のり
であることに着目し、以下の連立方程式を立てる。
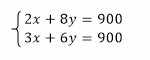
また、方程式は両辺に同じ値を乗じても成立することから、以下のように考えても良い。

これを解くと、
x=150,y=75
従って、走る速さは毎分150m,歩く速さは毎分75mである。
文章題の方程式を解く際は、以下の点を意識して下さい。
1.
状況を把握するために図にまとめる。
2.
方程式の解を求めた後、解を元の式に代入して(左辺)=(右辺)の成立を検証することにより検算できる。
3.
負の値になり得ない事柄(速さや商品の金額など)をxやyでおき、計算すると負の値になってしまった場合は、方程式の立て方が不適切だったり、計算ミスしていることを示している。このとき、これらの見直しが必要である。
計算の進め方は良くできていました。難易度が高めの問題に挑戦して、更なる向上を目指していきたいです。
 あゆむ学習室のサマースクールについては、こちらをご覧下さい。
あゆむ学習室のサマースクールについては、こちらをご覧下さい。


















