学年末試験（中２ 数学）で出題された難問

こんにちは。東久留米市の学習塾塾長です。

今日も良い天気になり、暖かい日が続きます。週の中頃は２０℃を超えるようで春らしくなってきました。

昨日は中２の塾生と数学の学年末試験のテスト見直しをしたのですが、そこに初等幾何の角度の問題（整角問題）で難問がありました。

図１にある平行四辺形で∠ＢＡＣ（ｘ）の角度を求める問題で、ヒントが付いていて、それは、「点ＡからＢＣに垂線ＡＥを引くと、ＡＥ＝ＡＯとなる」というものです。実は、この問題の類題が、難問揃いの「幾何大王からの挑戦状」にある程で、中学の学年末試験で解くのは大変だったと思います。

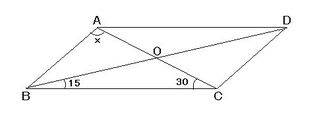
▲図１．中２学年末試験の難問

さて、解答です。取り敢えず、ヒントに従って、点ＡからＢＣに垂線ＡＥを引き、点Ｏと点Ｅを結びましょう。△ＯＥＣはＯＥ＝ＯＣの二等辺三角形で、また、平行四辺形の対角線は互いに２等分するので、ＯＡ＝ＯＣからＯＡ＝ＯＥとなります。つまり、△ＯＡＥは二等辺三角形になり、その一つの底角∠ＯＡＥは６０°なので、△ＯＡＥは正三角形になります。

つぎに、∠ＥＯＢ＝３０°－１５°＝１５°となるので、△ＥＢＯはＥＢ＝ＥＯの二等辺三角形になります。さらに、ＥＯ＝ＥＡですからＥＡ＝ＥＢとなり、△ＥＡＢも二等辺三角形で、その底角∠ＥＡＢ＝４５°なので、∠ＢＡＣ＝ｘ＝４５°＋６０°＝１０５°と正解に至ります。

▲図２．解答例

これくらいの難問をやっていれば、高校入試は楽でしょう。他の解法もあるので考えてみてください。