こんにちは。東久留米市の学習塾塾長です。
今回は、1986年AIMEの整数問題です。
問題は、
「数列 1,3,4,9,10,12,13,・・・は、3のべき乗(非負整数乗)と、相異なる3のべき乗の和で表わせる整数を小さい順に並べたものである。この数列の100番目の項はいくつか。ただし、1番目の項は 1、2番目の項は 3、・・・などと数えるものとする。」
です。
n個の3のべき乗の数
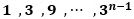
で表わすことができる数列の項数T(n)は、
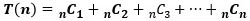
で、これは二項定理
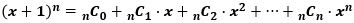
に x=1を代入することにより、

から

です。
ここで、

から、1、3、9、27、81、243 で表わせる数列の項数は63個です。
したがって、数列の63番目の項の値は、
1+3+9+27+81+243=364
になり、これは243×3=729より小さいので、729は1番目から63番目までの項には使われておらず、少なくとも64番目から値が1093(=1+3+9+27+81+243+729)になる項(127番目の項)まで連続して使われることになります。
また、

から、1、3、9、27、81、243、729 で表わせる数列の項数は127個です。
したがって、数列の127番目の項の値は、
1+3+9+27+81+243+729=1093
になり、これは729×3=2189より小さいので、2187は1番目から127番目までの項には使われません。
以上から数列の100番目の項は、1、3、9、27、81、243のなかのいくつかの数と729との和になります。
このとき729と、1、3、9、27、81で表わせる数列の項数は、

です。
したがって、数列の95番目(=63+32)の項の値は、
1+3+9+27+81+729=850
で、96番目の項は729+243=972になります。
ここまでで、数列の96番目の項が判ったので、あとは一つずつ勘定していくと、
96番目 : 729+243 =972
97番目 : 729+243+1 =973
98番目 : 729+243+3 =975
99番目 : 729+243+1+3=976
100番目 : 729+243+9 =981
になり、したがって数列の100番目の項は 981 で、これが答えです。
地道に項数を数え上げればOKです。
今回は、1986年AIMEの整数問題です。
問題は、
「数列 1,3,4,9,10,12,13,・・・は、3のべき乗(非負整数乗)と、相異なる3のべき乗の和で表わせる整数を小さい順に並べたものである。この数列の100番目の項はいくつか。ただし、1番目の項は 1、2番目の項は 3、・・・などと数えるものとする。」
です。
n個の3のべき乗の数
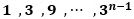
で表わすことができる数列の項数T(n)は、
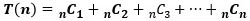
で、これは二項定理
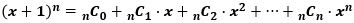
に x=1を代入することにより、

から

です。
ここで、

から、1、3、9、27、81、243 で表わせる数列の項数は63個です。
したがって、数列の63番目の項の値は、
1+3+9+27+81+243=364
になり、これは243×3=729より小さいので、729は1番目から63番目までの項には使われておらず、少なくとも64番目から値が1093(=1+3+9+27+81+243+729)になる項(127番目の項)まで連続して使われることになります。
また、

から、1、3、9、27、81、243、729 で表わせる数列の項数は127個です。
したがって、数列の127番目の項の値は、
1+3+9+27+81+243+729=1093
になり、これは729×3=2189より小さいので、2187は1番目から127番目までの項には使われません。
以上から数列の100番目の項は、1、3、9、27、81、243のなかのいくつかの数と729との和になります。
このとき729と、1、3、9、27、81で表わせる数列の項数は、

です。
したがって、数列の95番目(=63+32)の項の値は、
1+3+9+27+81+729=850
で、96番目の項は729+243=972になります。
ここまでで、数列の96番目の項が判ったので、あとは一つずつ勘定していくと、
96番目 : 729+243 =972
97番目 : 729+243+1 =973
98番目 : 729+243+3 =975
99番目 : 729+243+1+3=976
100番目 : 729+243+9 =981
になり、したがって数列の100番目の項は 981 で、これが答えです。
地道に項数を数え上げればOKです。










