こんにちは。東久留米市の学習塾塾長です。
今回は、2017年AIMEの組合せの問題です。
問題は、
「2017より小さい正の整数 n について、
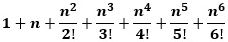
を整数とする n の個数を求めよ。」
です。
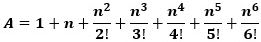
とすると、右辺の 1+n は整数なので、Aが整数になるためには、

が整数でなければなりません。
ここでBの右辺を通分すると、

になり、このとき分母は6の倍数であり、さらに分子の

は6の倍数なので、

も6の倍数でなければなりません。
そこで、
n=6k
とすると、kは、
1≦k≦336 (★)
の整数で、これをBの右辺に代入すると、

になります。
このとき右辺の
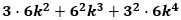
は整数なので、

が整数でなければならず、したがって、k、または、k+1 が5の倍数でなければなりません。
ここから、k が5の倍数の場合と k+1 が5の倍数の場合で場合分けして調べましょう。
● k が5の倍数の場合
k=5s
とすると、(★)から
1≦5s≦336 → 0.2≦s≦67.2
で、したがって、s は、1≦s≦67 の整数になり、これを満たす n の個数は67個です。
● k+1 が5の倍数の場合
k+1=5t → k=5t-1
とすると、(★)から
1≦5t-1≦336 → 0.4≦t≦67.4
で、したがって、t は、1≦t≦67 の整数になり、これを満たす n の個数は67個です。
以上から、Aを整数とする n の個数は、67+67= 134(個)で、これが答えです。
簡単な問題です。
今回は、2017年AIMEの組合せの問題です。
問題は、
「2017より小さい正の整数 n について、
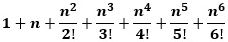
を整数とする n の個数を求めよ。」
です。
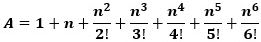
とすると、右辺の 1+n は整数なので、Aが整数になるためには、

が整数でなければなりません。
ここでBの右辺を通分すると、

になり、このとき分母は6の倍数であり、さらに分子の

は6の倍数なので、

も6の倍数でなければなりません。
そこで、
n=6k
とすると、kは、
1≦k≦336 (★)
の整数で、これをBの右辺に代入すると、

になります。
このとき右辺の
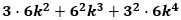
は整数なので、

が整数でなければならず、したがって、k、または、k+1 が5の倍数でなければなりません。
ここから、k が5の倍数の場合と k+1 が5の倍数の場合で場合分けして調べましょう。
● k が5の倍数の場合
k=5s
とすると、(★)から
1≦5s≦336 → 0.2≦s≦67.2
で、したがって、s は、1≦s≦67 の整数になり、これを満たす n の個数は67個です。
● k+1 が5の倍数の場合
k+1=5t → k=5t-1
とすると、(★)から
1≦5t-1≦336 → 0.4≦t≦67.4
で、したがって、t は、1≦t≦67 の整数になり、これを満たす n の個数は67個です。
以上から、Aを整数とする n の個数は、67+67= 134(個)で、これが答えです。
簡単な問題です。










