こんにちは。東久留米市の学習塾塾長です。
今回は、平成10年度東大入試問題(前期、文系)です。
問題は、
「xyz空間に3点

をとる。△ABCを1つの面とし、z≧0の部分に含まれる正四面体ABCDをとる。さらに△ABDを1つの面とし、点Cと異なる点Eをもう1つの頂点とする正四面体ABDEをとる。
(1)点Eの座標を求めよ。
(2)正四面体ABDEのy≦0の部分の体積を求めよ。」
です。
早速、取り掛かりましょう。
正四面体は4つの面がすべて正三角形で、図1のように、その1辺の長さを2とすると、各面の高さは
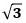
で、1つの頂点からその対面に垂線を下ろしその足をGとすると、Gは対面の重心(内心、外心、垂心)になり、垂線の長さ(高さ)は
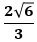
になります。(長さについては三平方の定理で簡単に計算できます)
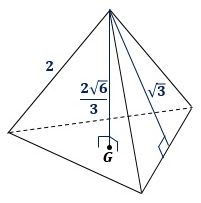
▲図1.正四面体(辺の長さ2)の特徴です
以上の正四面体の特徴を念頭に進めていきましょう。
正四面体ABCDはz≧0の部分にあるので、問題の図は図2のようになります。
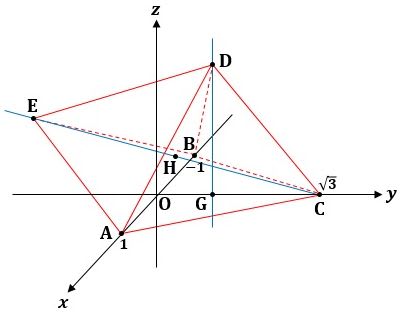
▲図2.問題の図を描きました
このとき、AB=2から正四面体ABCDの1辺の長さは2で、Dは正三角形ABCの重心Gの真上(z>0)にあり、その座標は
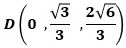
です。
次に図3のように、yz平面を観察しましょう。
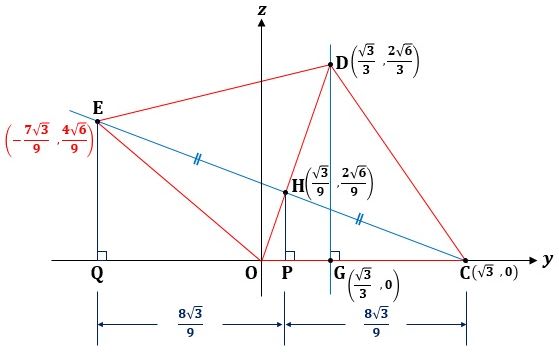
▲図3.yz平面を観察します
CおよびEから正三角形DABに垂線を下ろすとその足は、正三角形DABの重心Hになり、C、H、Eは同一直線上の点で、CH=HEが成り立ちます。
また、Hは線分ODを1:2に内分する点なので、その座標は
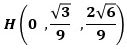
です。
ここで、H、Eからy軸に垂線を下ろしその足をそれぞれP、Qとすると、△CHP∽△CEQでその相似比は2なので、CP:CQ=1:2、
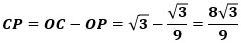
から
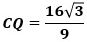
です。
すると、
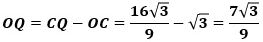
から、Eのy座標は

です。
さらに、HP:EQ=1:2、
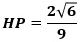
から
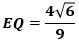
で、Eのz座標は
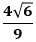
です。
したがって、Eの座標は
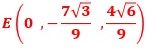
で、これが(1)の答えです。
続いて(2)です。
図4に示す三角錐E-RABの体積を求めることになります。
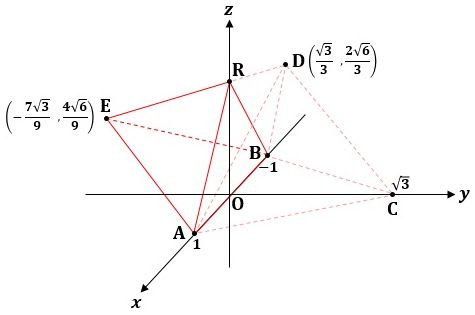
▲図4.三角錐E-RABの体積を求めます
三角錐E-RABの体積は、底面を△RABとすると高さがEのy座標の絶対値になるので、△RABの面積、つまり、Rのz座標を計算すれば簡単に求めることができます。
そこで図5のように、yz平面を調べましょう。
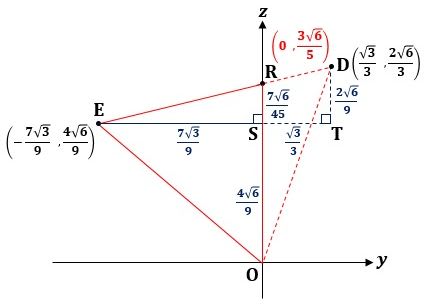
▲図5.Rのz座標を計算します
y軸に平行でEを通る直線とz軸との交点をS、Dから直線ESに下ろした垂線の足をTとすると、△ERS∽△EDTなので、ES:RS=ET:DTが成り立ち、
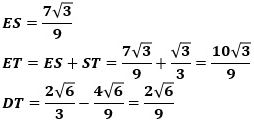
から
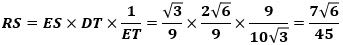
です。
すると、

から、Rのz座標は
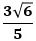
で、△RABの面積は
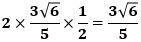
になります。
したがって、三角錐E-RABの体積は、
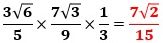
で、これが答えです。
簡単な問題です。
今回は、平成10年度東大入試問題(前期、文系)です。
問題は、
「xyz空間に3点

をとる。△ABCを1つの面とし、z≧0の部分に含まれる正四面体ABCDをとる。さらに△ABDを1つの面とし、点Cと異なる点Eをもう1つの頂点とする正四面体ABDEをとる。
(1)点Eの座標を求めよ。
(2)正四面体ABDEのy≦0の部分の体積を求めよ。」
です。
早速、取り掛かりましょう。
正四面体は4つの面がすべて正三角形で、図1のように、その1辺の長さを2とすると、各面の高さは
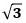
で、1つの頂点からその対面に垂線を下ろしその足をGとすると、Gは対面の重心(内心、外心、垂心)になり、垂線の長さ(高さ)は
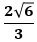
になります。(長さについては三平方の定理で簡単に計算できます)

▲図1.正四面体(辺の長さ2)の特徴です
以上の正四面体の特徴を念頭に進めていきましょう。
正四面体ABCDはz≧0の部分にあるので、問題の図は図2のようになります。

▲図2.問題の図を描きました
このとき、AB=2から正四面体ABCDの1辺の長さは2で、Dは正三角形ABCの重心Gの真上(z>0)にあり、その座標は
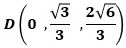
です。
次に図3のように、yz平面を観察しましょう。

▲図3.yz平面を観察します
CおよびEから正三角形DABに垂線を下ろすとその足は、正三角形DABの重心Hになり、C、H、Eは同一直線上の点で、CH=HEが成り立ちます。
また、Hは線分ODを1:2に内分する点なので、その座標は
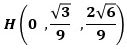
です。
ここで、H、Eからy軸に垂線を下ろしその足をそれぞれP、Qとすると、△CHP∽△CEQでその相似比は2なので、CP:CQ=1:2、
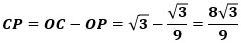
から
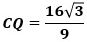
です。
すると、
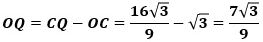
から、Eのy座標は

です。
さらに、HP:EQ=1:2、
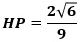
から
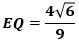
で、Eのz座標は
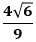
です。
したがって、Eの座標は
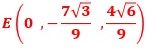
で、これが(1)の答えです。
続いて(2)です。
図4に示す三角錐E-RABの体積を求めることになります。

▲図4.三角錐E-RABの体積を求めます
三角錐E-RABの体積は、底面を△RABとすると高さがEのy座標の絶対値になるので、△RABの面積、つまり、Rのz座標を計算すれば簡単に求めることができます。
そこで図5のように、yz平面を調べましょう。

▲図5.Rのz座標を計算します
y軸に平行でEを通る直線とz軸との交点をS、Dから直線ESに下ろした垂線の足をTとすると、△ERS∽△EDTなので、ES:RS=ET:DTが成り立ち、
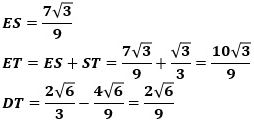
から
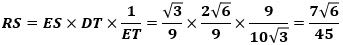
です。
すると、

から、Rのz座標は
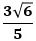
で、△RABの面積は
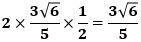
になります。
したがって、三角錐E-RABの体積は、
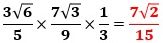
で、これが答えです。
簡単な問題です。










