こんにちは。東久留米市の学習塾塾長です。
晴れているのですが陽射しは弱く少し寒々とした日になりました。今日から冬期講習の後半が始まります。
先日、雪の結晶の話題を取り上げたとき、平面に敷き詰めることができる正多角形は、正三角形、正四角形および正六角形だけと紹介しました。これは平面上のある点に正多角形の頂点を合わせて並べた場合、正多角形同士が重なりもせず、かつ隙間なく並べることができるのは、正多角形の内角の整数倍が360°になる場合であることから分かります。
それでは3次元空間を隙間なく埋め尽くすことができる正多面体についてはどうでしょうか。正多面体は、正四面体、正六面体、正八面体、正十二面体および正二十面体の5つありますが、このうち正六面体だけが可能です。
どうしてそうなるかと言うと、平面と正多角形の場合に頂点に着目したのに対して、空間と正多面体の場合には正多面体の辺に着目します。正多面体同士の辺を重ねた場合、その辺の周りに正多面体が隙間なく埋め尽くすことができるのは、正多面体の二面角の整数倍が360°になる場合です。
正多面体の二面角は、辺を共有する面のなす角です。図に正四面体の場合を示します。この二面角を計算すると、正四面体:70.5288°、正六面体:90°、正八面体:109.4712°、正十二面体:116.5652°、正二十面体:138.1898°となり、これらの二面角を整数倍して360°にできるのは正六面体だけと分かります。
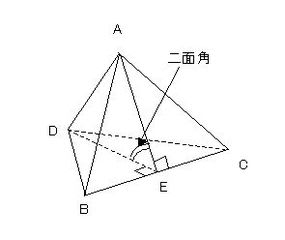
▲正四面体の二面角
実はこの問題について、あの有名なアリストテレスは正四面体と正六面体の二つが空間を隙間なく埋め尽くせると主張していて間違えていたようで、この問題が最終的に解決するのは17世紀になってからです。
晴れているのですが陽射しは弱く少し寒々とした日になりました。今日から冬期講習の後半が始まります。
先日、雪の結晶の話題を取り上げたとき、平面に敷き詰めることができる正多角形は、正三角形、正四角形および正六角形だけと紹介しました。これは平面上のある点に正多角形の頂点を合わせて並べた場合、正多角形同士が重なりもせず、かつ隙間なく並べることができるのは、正多角形の内角の整数倍が360°になる場合であることから分かります。
それでは3次元空間を隙間なく埋め尽くすことができる正多面体についてはどうでしょうか。正多面体は、正四面体、正六面体、正八面体、正十二面体および正二十面体の5つありますが、このうち正六面体だけが可能です。
どうしてそうなるかと言うと、平面と正多角形の場合に頂点に着目したのに対して、空間と正多面体の場合には正多面体の辺に着目します。正多面体同士の辺を重ねた場合、その辺の周りに正多面体が隙間なく埋め尽くすことができるのは、正多面体の二面角の整数倍が360°になる場合です。
正多面体の二面角は、辺を共有する面のなす角です。図に正四面体の場合を示します。この二面角を計算すると、正四面体:70.5288°、正六面体:90°、正八面体:109.4712°、正十二面体:116.5652°、正二十面体:138.1898°となり、これらの二面角を整数倍して360°にできるのは正六面体だけと分かります。

▲正四面体の二面角
実はこの問題について、あの有名なアリストテレスは正四面体と正六面体の二つが空間を隙間なく埋め尽くせると主張していて間違えていたようで、この問題が最終的に解決するのは17世紀になってからです。










