今回は、手首の細い接続軸が目立つのを隠すカバーを設計します、三平方の定理(ピタゴラスの定理とも言う)を理解しておくと、設計方法が良く理解できます
三平方の定理(ピタゴラスの定理)
直角三角形の斜辺の2乗は他の2辺の2乗の和と等しい
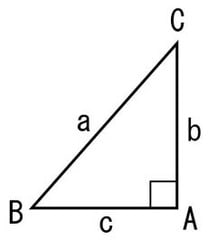
a×a=b×b+c×c
2乗の打ち方が分らないので、式の書き方が変なのはご容赦下さい
ボールジョイントはWAVEのボールジョイントを使用します

今、このタイプのボールジョイントは売っていないようです、あまり参考にならなくて申し訳ない
ボールジョイントをノギスで測定します
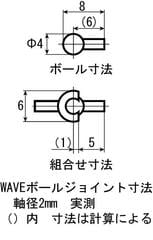
拳と前腕を測定して取付位置を検討します

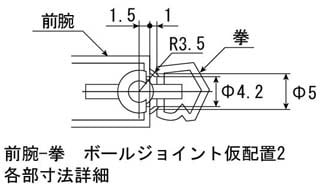
拳には5mm径の穴加工が最大で、前腕との間隔を1mm、ボールジョイントの受けを前腕の先端と面位置にしてみます
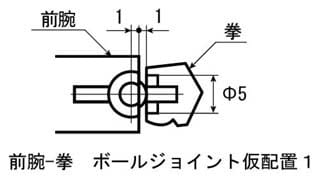
三平方の定理でボールジョイントカバーの半径を計算します
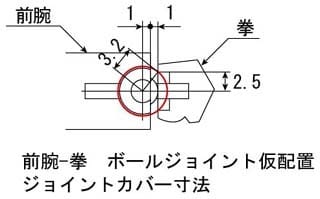
√((1+1)×(1+1)+2.5×2.5)=3.2015
カバー半径3.2mm 図の赤い線の部分
ボールジョイント受けの直径が6mmなので、これだと接着シロがほとんどないため、今度はボールジョイントの受けを前腕先端から0.5mm奥まったところにします
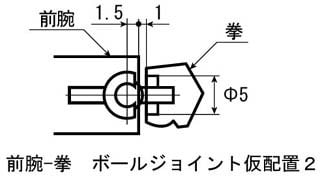
同様にして、三平方の定理でボールジョイントカバーの半径を計算します

√((1.5+1)×(1.5+1)+2.5×2.5)=3.5355
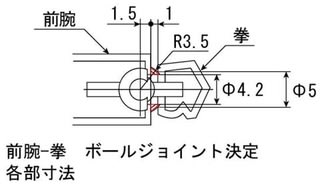
カバー半径3.5mm 図の赤い線の部分
今度は問題ありません
更に形状を細かく検討します
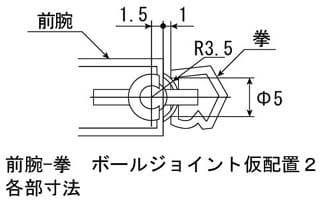
可動範囲を作図してカバーにあける取付穴の大きさを検討します
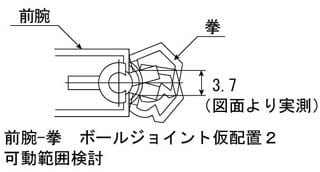
直径3.7mm必要です、拳の作図は不正確なので、多少のずれがあると思います
ボールジョイントのボール径が4mmなので、カバーにあける取付穴は少し大きめの4.2mmにします
4.2mm穴にしたときの可動範囲を調べます
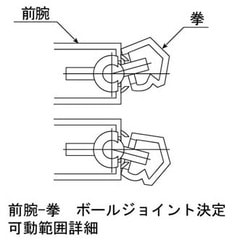
最大に稼動させた時、隙間が見えるのが分ります、でもこの部品の大きさはどのくらいでしょうか
調べると直径6.3mm、厚さ1.3mmです、このような小さい部品を加工するのは困難です、何か流用できるものはないかと調べると、コトブキヤの丸モールド6mmが使用できそうです、コトブキヤの丸モールド6mmに4.2mm穴をあけるのでも小さ過ぎて困難だと思いますが

寸法をノギスで計測して、表面の曲率半径を計算します
上 実測値、下 計算のための補助線
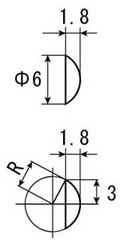
曲率半径をRとすると
R×R=(R-1.8)×(R-1.8)+3×3 となります、この方程式の解が曲率半径です
解 R=3.4
これを作図してみるとこのような感じになります、図の赤い線

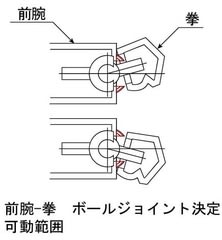
形状が小さくなって、隙間が更に開いた感じになりましたが、これで決定にします
このように、計算ではいくらでも細かくできますが、うちではこのように高精度で製作することはできません、結局は現物合わせになってしまうと思います、そのようなことに、こんなに工数をかけてしまうとは、あほみたいです
次回は、実際に製作してみます
今回ここまで
次の回を読む
1/144ガンダム 旧キット製作7回(ポリキャップ組込み4 拳、前腕、肘)
前の回を読む
1/144ガンダム 旧キット製作5回(ポリキャップ組込み2 ビームサーベル、拳)
第1回から読む
1/144ガンダム 旧キット製作1回(キットの解説1)
三平方の定理(ピタゴラスの定理)
直角三角形の斜辺の2乗は他の2辺の2乗の和と等しい

a×a=b×b+c×c
2乗の打ち方が分らないので、式の書き方が変なのはご容赦下さい
ボールジョイントはWAVEのボールジョイントを使用します

今、このタイプのボールジョイントは売っていないようです、あまり参考にならなくて申し訳ない
ボールジョイントをノギスで測定します

拳と前腕を測定して取付位置を検討します

拳には5mm径の穴加工が最大で、前腕との間隔を1mm、ボールジョイントの受けを前腕の先端と面位置にしてみます

三平方の定理でボールジョイントカバーの半径を計算します

√((1+1)×(1+1)+2.5×2.5)=3.2015
カバー半径3.2mm 図の赤い線の部分
ボールジョイント受けの直径が6mmなので、これだと接着シロがほとんどないため、今度はボールジョイントの受けを前腕先端から0.5mm奥まったところにします

同様にして、三平方の定理でボールジョイントカバーの半径を計算します

√((1.5+1)×(1.5+1)+2.5×2.5)=3.5355
カバー半径3.5mm 図の赤い線の部分
今度は問題ありません
更に形状を細かく検討します

可動範囲を作図してカバーにあける取付穴の大きさを検討します

直径3.7mm必要です、拳の作図は不正確なので、多少のずれがあると思います
ボールジョイントのボール径が4mmなので、カバーにあける取付穴は少し大きめの4.2mmにします

4.2mm穴にしたときの可動範囲を調べます

最大に稼動させた時、隙間が見えるのが分ります、でもこの部品の大きさはどのくらいでしょうか
調べると直径6.3mm、厚さ1.3mmです、このような小さい部品を加工するのは困難です、何か流用できるものはないかと調べると、コトブキヤの丸モールド6mmが使用できそうです、コトブキヤの丸モールド6mmに4.2mm穴をあけるのでも小さ過ぎて困難だと思いますが

寸法をノギスで計測して、表面の曲率半径を計算します
上 実測値、下 計算のための補助線

曲率半径をRとすると
R×R=(R-1.8)×(R-1.8)+3×3 となります、この方程式の解が曲率半径です
解 R=3.4
これを作図してみるとこのような感じになります、図の赤い線


形状が小さくなって、隙間が更に開いた感じになりましたが、これで決定にします
このように、計算ではいくらでも細かくできますが、うちではこのように高精度で製作することはできません、結局は現物合わせになってしまうと思います、そのようなことに、こんなに工数をかけてしまうとは、あほみたいです
次回は、実際に製作してみます
今回ここまで
次の回を読む
1/144ガンダム 旧キット製作7回(ポリキャップ組込み4 拳、前腕、肘)
前の回を読む
1/144ガンダム 旧キット製作5回(ポリキャップ組込み2 ビームサーベル、拳)
第1回から読む
1/144ガンダム 旧キット製作1回(キットの解説1)


























まさに設計に値します。
普段自分が起こしてる図面とかはホントにスケッチみたいなもんなんで、益々尊敬。
いや、怖いくらいです( ̄□ ̄;)
図面はブログ用に清書したもので、通常は鉛筆で描いたラフスケッチです、そのためますます工数がかかってしまいました、計算より、図面清書の方が工数かかっています
最後に書いていますが、加工精度が追いついていないので、この後がたがたになると思います、工数かけた計算のほとんどは、あまり意味ないものになります、設計には製造可能かとか全体をみて、精度等を調整するバランス感覚が重要になります