確率問題の解き方

こんにちは。東久留米市の学習塾塾長です。

冷たい雨が降っていて気温も低くなりました。卒業式には少し残念な天気です。近頃の中学卒業生は、学校行事の後、「打ち上げ」をするそうで、私の頃とは隔世の感があります。

さて、今日は中２数学の確率の話題です。１９８６年の防衛医大の問題で、「重さの異なる４個の玉が入っている袋から玉を一つ取り出し、元に戻さずにもう１つの玉を取り出したところ、２番目の玉の方が重かった。２番目の玉が４個の中で最も重い確率を求めよ」というものです。

簡単に片付けると、４つの玉を２つずつ２つに分けたとき、一方に最も重い玉がある確率ですから１/２が答えになります。

これを中２で勉強する（実際には、小６でも勉強しているのですが）樹形図で解いてみます。

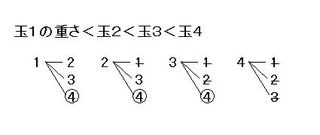
▲図１．樹形図

玉の軽いほうから、玉１＜玉２＜玉３＜玉４として、初めに取り出した玉と２番目に取り出した玉で図１にあるような樹形図を作ります。初めに取り出した玉より２番目に取り出した玉が重いので、２－１、３－１、３－２、４－１、４－２、４－３の事象はありえません。つまり、すべての場合の数は６通りになります。また、２番目に取り出した玉が一番重いとは、２番目に玉４を取り出すことなので、図の○をつけた事象の３通りになります。つまり、確率は、３/６＝１/２となります。

次に、高校で勉強する条件付き確率で解いてみましょう。２番目の玉が初めに取り出した玉より重いという事象をＡ、２番目の玉が４個の中で一番重いという事象をＢとすると、図２のように事象Ａが起こったという条件のもとで事象Ｂが起きる確率ＰA（Ｂ）は、１/２となります。

▲図２．条件付き確率

ここで同時確率Ｐ（Ａ∩Ｂ）がＰ（Ｂ）となることに注意してください。つまり、２番目に取り出した玉が初めに取り出した玉より重いという事象（事象Ａ）は、２番目に取り出した玉が４つの中で一番重いという事象（事象Ｂ）に含まれているということです。

一番最初の解き方がスマートだと思いますが、樹形図を使った解法が判り易いかもしれません。いずれにしろ、数学の問題には、いろいろな解き方があるので、複数の解法を考えてみると勉強になります。