ヨーテボリ大学ジャーナリズム学部 (Department of Journalism, Media and Communication) のケント・アスプ教授は、マスメディアによる選挙報道の研究で知られるが、2年ほど前に発表された研究がちょっとした話題を呼んだ。
この研究は、スウェーデン国内のジャーナリストの支持政党を調査したものだが、控えめに言っても非常に物議を醸す研究だった。タイトルは『ジャーナリスト集団の支持政党』で、ここではスウェーデン国内のメディアで働くジャーナリストのうち、2362人にアンケートを行い、どの党が好みかを調査している。その結果は、
このように、圧倒的に環境党を選んだジャーナリストが多かったのである。この結果にもとづき、アスプ教授は「スウェーデンのジャーナリストが政治論争を報道する時に、環境党が贔屓される恐れがあるではないか」と結論づけた。
ただ、アンケートの対象が2362人であるのに対し、実際に回答したのは1338人であり、回答率は56.6%である(ただ、別の箇所には回答者数1301人とあり不整合。また、2362人は論文には明記されておらず、付録としてスウェーデン・テレビに提出した書類に書かれているという)。非回答者があまりに多いため、結果を一般化するのには無理があるのではないか? まず、この点が批判された。
しかし、それ以上に注目を浴びたのは、メディアごとの内訳である。論文の中では主要メディアごとの統計も掲載されているのだが、公共放送であるスウェーデン・テレビ(SVT)に至っては、回答者のうち52%が環境党と答えているのである。
果たして、SVTのジャーナリストの過半数が、環境党を支持しているのか!?
この研究結果に、先日、SVTの有名政治記者が大きな問題提起を行った。この記者の論点はこうだ。
すると、まもなくしてアスプ教授が反論した。(括弧内は私のコメント)
このように、非常におかしな回答であると私は思う。問題提起を行ったSVTの政治記者も全く納得していない。また、同じく公共放送であるスウェーデン・ラジオでも、環境党が54%とさらに突出しているが、スウェーデン・ラジオの社長も少し前に反論している。彼は、仮にニュースや報道に携わるジャーナリストに環境党のシンパが多かったとしても、それと、ジャーナリストとしての職業モラルは別物である。まともなジャーナリストであれば、自分の政治選好を拠り所として、ジャーナリストの仕事をすることはない、と指摘している。
ここまでは、実は今回の記事の前置き。
上に示した議論以上に面白かったのは、外野によるSVTの政治記者へのツッコミだ。
さて、どうだろう? これは統計学をきちんと勉強したかどうかをチェックする、非常に良い問題だと思う。果たして、93人のSVTジャーナリストから回答を得たアスプ教授の調査のほうが、2000人から回答を得た世論調査よりも信頼性が高いのか?
もちろん、非回答率の問題やランダム性の問題があるので、ここでは仮に両方の調査において、回答者である93人および2000人がランダムに選ばれていると仮定して議論したい。また、アスプ教授の調査も有権者の支持動向を問う世論調査も、回答の選択肢は複数ある(例、環境党、社会民主党、自由党、etc)が、計算が非常に面倒になるので、計算を楽にするため、選択肢は2つしかないものと仮定する(つまり、「支持する」vs「支持しない」)。
では、信頼性の問題を考えるために、以下の2つのケースを想定してみたい。
(A) 母集団が1,100人であり、ランダムに選んだ93人にアンケートをしたところ、52%が「支持する」と答えた。
(B) 母集団が7,000,000人であり、ランダムに選んだ2000人にアンケートをしたところ、52%が「支持する」と答えた。
さて、どちらの調査結果のほうが信頼性が高いだろうか? 母集団に対するサンプルの大きさが大きい (A)のほうだろうか?
この答えは、信頼区間を求めれば分かる。
信頼区間の幅を決める標準誤差は、以下の式で求められる。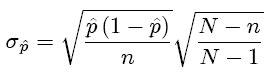
だから、(A)の標準誤差は となり、95%の信頼区間は、
となり、95%の信頼区間は、 となる。つまり、母集団における支持率は95%の確率でこの2つの値(42.3%と61.7%)の間に存在するということである。
となる。つまり、母集団における支持率は95%の確率でこの2つの値(42.3%と61.7%)の間に存在するということである。
一方、(B)の標準誤差は となる。( n/N の比率が0.05以下の場合、二つ目のルートの部分はほぼ1になるので、無視してもよい)
となる。( n/N の比率が0.05以下の場合、二つ目のルートの部分はほぼ1になるので、無視してもよい)
95%の信頼区間は、 となる。つまり、母集団における支持率は95%の確率でこの2つの値(49.8%と54.2%)の間に存在するということである。
となる。つまり、母集団における支持率は95%の確率でこの2つの値(49.8%と54.2%)の間に存在するということである。
結論として、(B)のケースのほうが信頼性が高いのである。母集団(N)に対するサンプルサイズ(n)の大きさは、その比率があまり大きくない場合、信頼性(つまり、標準誤差の大きさ)に意味を持たないということである。
ちなみに、(A)のケースにおいて、サンプルサイズをどれだけ大きくすれば、(B)のケースと同じだけの信頼性が得られるのかを調べてみたい。

Y軸は標準誤差、X軸はサンプルサイズ(n)を示している。(A)の標準誤差を(B)の標準誤差である0.0112まで小さくするには、n=710、つまり、710人もの人にアンケートをしなければならないのである。
このツッコミをした人は自信満々だったが、統計学をちゃんと学んでいないのであろう。標準誤差や信頼区間は、大学1年生向けの初級の統計学で教えている内容である。
この研究は、スウェーデン国内のジャーナリストの支持政党を調査したものだが、控えめに言っても非常に物議を醸す研究だった。タイトルは『ジャーナリスト集団の支持政党』で、ここではスウェーデン国内のメディアで働くジャーナリストのうち、2362人にアンケートを行い、どの党が好みかを調査している。その結果は、
環境党:41%
左党:15%
穏健党:14%
社会民主党:14%
自由党:7%
中央党:4%
キリスト教民主党:2%
左党:15%
穏健党:14%
社会民主党:14%
自由党:7%
中央党:4%
キリスト教民主党:2%
このように、圧倒的に環境党を選んだジャーナリストが多かったのである。この結果にもとづき、アスプ教授は「スウェーデンのジャーナリストが政治論争を報道する時に、環境党が贔屓される恐れがあるではないか」と結論づけた。
ただ、アンケートの対象が2362人であるのに対し、実際に回答したのは1338人であり、回答率は56.6%である(ただ、別の箇所には回答者数1301人とあり不整合。また、2362人は論文には明記されておらず、付録としてスウェーデン・テレビに提出した書類に書かれているという)。非回答者があまりに多いため、結果を一般化するのには無理があるのではないか? まず、この点が批判された。
しかし、それ以上に注目を浴びたのは、メディアごとの内訳である。論文の中では主要メディアごとの統計も掲載されているのだが、公共放送であるスウェーデン・テレビ(SVT)に至っては、回答者のうち52%が環境党と答えているのである。
果たして、SVTのジャーナリストの過半数が、環境党を支持しているのか!?
この研究結果に、先日、SVTの有名政治記者が大きな問題提起を行った。この記者の論点はこうだ。
・SVTには全部で約1100人のジャーナリストがいるが、回答者はわずか93人。この93人の回答をもって、1100人全員の政党支持傾向がどこまで言えるのか? サンプルが果たしてランダムであるのか?
・「ジャーナリスト」という職業タイトルは、(スウェーデンでは)ニュース・報道を担当する記者だけでなく、マスメディアの様々な活動の企画から進行に関わるすべての人に使われる。だから、回答者が報道に関わっているとは限らず、子供番組の企画をしている職員かもしれないし、スポーツ番組のレポーターや、バラエティー担当や音声担当の人かもしれない。もし、そうであれば、仮に彼らの多数が環境党支持者であっても、報道にバイアスが掛かる心配はない。研究結果にはその点が明らかにされていない。
・まともな政治記者なら「支持政党はどこか?」などというアンケートには、職業モラルから答えない。自分も今まで何度かそのようなアンケートを受け取ったが、答えることなく、すぐにゴミ箱に捨てた。自分の同僚で政治報道に関わる記者に尋ねても、アンケートに答えたという人は誰もいない。回答したという93人の大部分は報道以外に携わるジャーナリストなのではないか?
・「ジャーナリスト」という職業タイトルは、(スウェーデンでは)ニュース・報道を担当する記者だけでなく、マスメディアの様々な活動の企画から進行に関わるすべての人に使われる。だから、回答者が報道に関わっているとは限らず、子供番組の企画をしている職員かもしれないし、スポーツ番組のレポーターや、バラエティー担当や音声担当の人かもしれない。もし、そうであれば、仮に彼らの多数が環境党支持者であっても、報道にバイアスが掛かる心配はない。研究結果にはその点が明らかにされていない。
・まともな政治記者なら「支持政党はどこか?」などというアンケートには、職業モラルから答えない。自分も今まで何度かそのようなアンケートを受け取ったが、答えることなく、すぐにゴミ箱に捨てた。自分の同僚で政治報道に関わる記者に尋ねても、アンケートに答えたという人は誰もいない。回答したという93人の大部分は報道以外に携わるジャーナリストなのではないか?
すると、まもなくしてアスプ教授が反論した。(括弧内は私のコメント)
・回答率は60%以上であり、問題ない。(← ん? どうして60%以上という計算になる?)
・国内のメディアで働くジャーナリスト全体に占めるSVTのジャーナリストの割合を考えれば、回答者1338人のうちSVTジャーナリストが93人しかいないのはおかしなことではない。(← しかし、サンプル数が少ない上に、SVTの回答率やランダム性が明らかではないので、メディアごとの数字を論文に掲載すべきではないのでは? しかも、アスプ教授は掲載するだけではなくて、SVTが特に偏っている、という趣旨の議論を始めている。)
・このアンケートで尋ねているのは「今の時点でどの政党を最も好むか?」であり、「どの政党の支持者か?」ではない。アンケートを行ったのは2011年で、ちょうど社会民主党の党首がスキャンダルにまみれて、退陣に追い込まれた時であるから、本来、社会民主党を支持するジャーナリストが環境党を選んだ可能性もあり、それが環境党が突出した原因であろう。(← ん? じゃあ、なぜ『ジャーナリスト集団の支持政党』などというタイトルを付けるの?)
・国内のメディアで働くジャーナリスト全体に占めるSVTのジャーナリストの割合を考えれば、回答者1338人のうちSVTジャーナリストが93人しかいないのはおかしなことではない。(← しかし、サンプル数が少ない上に、SVTの回答率やランダム性が明らかではないので、メディアごとの数字を論文に掲載すべきではないのでは? しかも、アスプ教授は掲載するだけではなくて、SVTが特に偏っている、という趣旨の議論を始めている。)
・このアンケートで尋ねているのは「今の時点でどの政党を最も好むか?」であり、「どの政党の支持者か?」ではない。アンケートを行ったのは2011年で、ちょうど社会民主党の党首がスキャンダルにまみれて、退陣に追い込まれた時であるから、本来、社会民主党を支持するジャーナリストが環境党を選んだ可能性もあり、それが環境党が突出した原因であろう。(← ん? じゃあ、なぜ『ジャーナリスト集団の支持政党』などというタイトルを付けるの?)
このように、非常におかしな回答であると私は思う。問題提起を行ったSVTの政治記者も全く納得していない。また、同じく公共放送であるスウェーデン・ラジオでも、環境党が54%とさらに突出しているが、スウェーデン・ラジオの社長も少し前に反論している。彼は、仮にニュースや報道に携わるジャーナリストに環境党のシンパが多かったとしても、それと、ジャーナリストとしての職業モラルは別物である。まともなジャーナリストであれば、自分の政治選好を拠り所として、ジャーナリストの仕事をすることはない、と指摘している。
※ ※ ※ ※ ※
ここまでは、実は今回の記事の前置き。
上に示した議論以上に面白かったのは、外野によるSVTの政治記者へのツッコミだ。
1100人のSVTジャーナリストに対して回答者が93人というのは少なすぎるというけど、あなたが日頃、報道で取り上げる世論調査の回答者はせいぜい2000人じゃないか!
1100人に占める93人の割合は8.45% (= 93 / 1,100) だけど、有権者全員(700万人)に占める2,000人の割合は、それよりもずーっと小さくて、わずか0.0285 % (= 2,000 / 7,000,000) だ。こんな小さな割合にもかかわらず、世論調査ではその2000人の回答をもとに有権者全体の支持動向を分析し、あなたも真面目にニュースに取り上げているではないか。そんなあなたが、アスプ教授の研究を「サンプルが小さい」と批判するのは、全くもって滑稽だ。
1100人に占める93人の割合は8.45% (= 93 / 1,100) だけど、有権者全員(700万人)に占める2,000人の割合は、それよりもずーっと小さくて、わずか0.0285 % (= 2,000 / 7,000,000) だ。こんな小さな割合にもかかわらず、世論調査ではその2000人の回答をもとに有権者全体の支持動向を分析し、あなたも真面目にニュースに取り上げているではないか。そんなあなたが、アスプ教授の研究を「サンプルが小さい」と批判するのは、全くもって滑稽だ。
さて、どうだろう? これは統計学をきちんと勉強したかどうかをチェックする、非常に良い問題だと思う。果たして、93人のSVTジャーナリストから回答を得たアスプ教授の調査のほうが、2000人から回答を得た世論調査よりも信頼性が高いのか?
もちろん、非回答率の問題やランダム性の問題があるので、ここでは仮に両方の調査において、回答者である93人および2000人がランダムに選ばれていると仮定して議論したい。また、アスプ教授の調査も有権者の支持動向を問う世論調査も、回答の選択肢は複数ある(例、環境党、社会民主党、自由党、etc)が、計算が非常に面倒になるので、計算を楽にするため、選択肢は2つしかないものと仮定する(つまり、「支持する」vs「支持しない」)。
では、信頼性の問題を考えるために、以下の2つのケースを想定してみたい。
(A) 母集団が1,100人であり、ランダムに選んだ93人にアンケートをしたところ、52%が「支持する」と答えた。
(B) 母集団が7,000,000人であり、ランダムに選んだ2000人にアンケートをしたところ、52%が「支持する」と答えた。
さて、どちらの調査結果のほうが信頼性が高いだろうか? 母集団に対するサンプルの大きさが大きい (A)のほうだろうか?
この答えは、信頼区間を求めれば分かる。
信頼区間の幅を決める標準誤差は、以下の式で求められる。
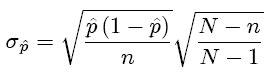
だから、(A)の標準誤差は


一方、(B)の標準誤差は

95%の信頼区間は、

結論として、(B)のケースのほうが信頼性が高いのである。母集団(N)に対するサンプルサイズ(n)の大きさは、その比率があまり大きくない場合、信頼性(つまり、標準誤差の大きさ)に意味を持たないということである。
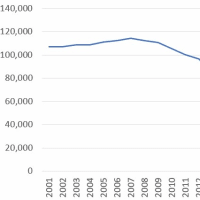
ちなみに、(A)のケースにおいて、サンプルサイズをどれだけ大きくすれば、(B)のケースと同じだけの信頼性が得られるのかを調べてみたい。

Y軸は標準誤差、X軸はサンプルサイズ(n)を示している。(A)の標準誤差を(B)の標準誤差である0.0112まで小さくするには、n=710、つまり、710人もの人にアンケートをしなければならないのである。
このツッコミをした人は自信満々だったが、統計学をちゃんと学んでいないのであろう。標準誤差や信頼区間は、大学1年生向けの初級の統計学で教えている内容である。

















※コメント投稿者のブログIDはブログ作成者のみに通知されます