1.まえがき
座標系の原点をOとする。直線l: y=3x/4 上の点A(4,3)で、lに接する円をC₁とする。
C₁は +x軸とも接する。円C₂は直線lについて円C₁と線対象である。円C₁上の点Pが点A
について点対称のC₂上の点をQとする。
このとき、円C₁の式と、三角形OPQの面積が 25/3 となるとき、直線 PQの傾きを求め
よ。
2.計算
(1) C₁の式
円C₁の中心を(a,b)とする。つまり
C₁: (x-a)²+(y-b)²=b²・・・・・①
となる。これをxで微分して、この円の接線の傾きy'は
x-a+(y-b)y'=0 → y'=-(x-a)/(y-b)
となる。
これが、A(4,3)でlと接すると傾きは 3/4になるから
y'=-(x-a)/(y-b)=-(4-a)/(3-b)=3/4 → 4a+3b=25・・・・②
また、AはC₁上にもあるから、①により
(4-a)²+(3-b)²=b²
となり、②を入れてbを消すと
a²=25 → a=5 (>0)
を得る。②から
b=5/3
ゆえに
C₁: (x-5)²+(y-5/3)²=(5/3)²・・・・・③
(2) 直線PQの傾き
点対称だから、長さ QA=AP であり、3角形 OAQとOAP の面積は等しい。だから
求める3角形OPQの面積Sは、ベクトルOP=<x,y> と OA=<4,3> の外積で表される
平行四辺形の面積だから
S=|<x,y>×<4,3>|=|3x-4y|=3x-4y=25/3
となる(この順のベクトル積は+z方向となり、3x-4y≧0)。これに、④を入れると
y=3x/4-25/12・・・・・⑤
これを③に入れてまとめると
x²-10x+25+(3x/4-25/12-5/3)²=25/9 → x²-10x+25+(3x/4-15/4)²=25/9
→ (1+9/16)x²-(10+45/8)x+25+(15/4)²-25/9=0
→ 25x²-250x+16・25+15²-16・25/9=0 → x²-10x+16+15²/25-16/9=0
→ x²-10x+209/9=0 → x=5±4/3=11/3, 19/3
⑤にいれて
(x,y)=(11/3,2/3), (19/3,8/3)
PQの傾きmは
(11/3,2/3)のとき m=(3-y)/(4-x)=7
(19/3,8/3)のとき m=(3-y)/(4-x)=-1/7
3.あとがき
上のように、2つの傾きは直行している。AP、AQが円の直径と一致するとき、3角
形OPQの面積は最大
OA・AP=5・(5/3)・2=50/3
となる。PQの角度が時計・反時計回りの2方向に変化していくとき3角系の面積は
0になっていく。
以上
最新の画像[もっと見る]
-
 電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
-
 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
-
 x² 上の任意の2つの点の法線の交点の作る集合
3年前
x² 上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
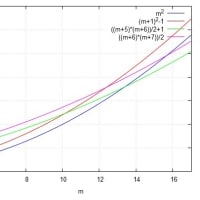 とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
-
 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
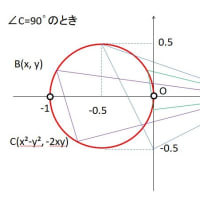 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
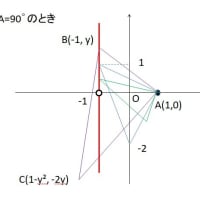 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
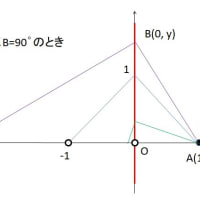 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
「算数」カテゴリの最新記事
 長方形の中心を通り、直交する2直線によって、等分割する問題
長方形の中心を通り、直交する2直線によって、等分割する問題 sin/cosを含む連立方程式の解法
sin/cosを含む連立方程式の解法 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件 ある線分とパラメータa,bで表される円があるとき、円が線分を含まないa,bの範囲
ある線分とパラメータa,bで表される円があるとき、円が線分を含まないa,bの範囲 円の外部にある点Pから、その円への接線との交点の中点をQとする。Pが移動するとき...
円の外部にある点Pから、その円への接線との交点の中点をQとする。Pが移動するとき... 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡...
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡... 2つの曲線 y=x² と y=(x-a)²/4 (a>0)で囲まれた領域で x+2y の最大最小値
2つの曲線 y=x² と y=(x-a)²/4 (a>0)で囲まれた領域で x+2y の最大最小値 放物線が放物線上を転がるときの軌跡
放物線が放物線上を転がるときの軌跡 ある変数変換に対する領域の形状変化
ある変数変換に対する領域の形状変化 x,yの多項式 f(x,y)が f(x,y)=f(y,x) を満たすときの形式
x,yの多項式 f(x,y)が f(x,y)=f(y,x) を満たすときの形式














