こんにちは。東久留米市の学習塾塾長です。
朝TVでは昨日より寒さが和らぐと言っていましたが、今日も充分寒いです。
中1の数学の授業で、「三角形の五心」を勉強しているということで、塾生とそれらの作図をしました。五心のうちの内心、外心、重心は、高校の数学Aで扱うので、中学の教科書には載っていませんが、きっと幾何学好きの先生なのでしょう。
五心のなかでも重心は身近な存在で、三角形の板を指の先にのせてバランスを取ると、その指の先が重心の位置になります。これは三角形に限ったことではなく、均質な板で作った任意の図形にあてはまることです。
三角形の重心の作図による求め方は、各頂点と対辺の中点を結ぶと3本の直線(中線といいます)が1点で交わり、この点を重心と言います。
また、重心は3本の中線を2:1に内分します。これは、直線上にない3つの同じ重さの錘を考えた場合、2つの錘の重心はそれらの中点で重さは2倍になります(「やじろべえ」です)。次に、それと残りの錘の重心を考えると、重心の位置はそれらを結んだ線分上にありますが、重さの比が2:1なので、その線分を1:2に内分する点になるということです。
ところで、最初に戻って「中線が1点で交わる」ということを証明するのは慣れていないと難しいかもしれません。と言うのは、中学校で勉強する図形の証明では、辺の長さや角の大きさが等しいことの証明などが多く、直線が1点で交わることの証明や3点が直線上にあることの証明などにお目にかかることはありません。
そこで、一例として三角形の中線が1点で交わることの証明を簡単に紹介します。
下図で点D、Eはそれぞれ辺BC、CAの中点で、ADとBEとの交点をGとします。そこで、DEを結ぶと、中点連結定理により、AB//EDで、AB:ED=2:1です。また、△GAB∽△GDEなので、BEはADを2:1に内分する点Gで交わります。
同様に、辺ABの中点Fとして、ADとCFとの交点をG’とすると、△G’AC∽△G’DFとなるので、CFはADを2:1に内分する点G’で交わります。
つまり、点Gも点G’もADを2:1に内分する点なので点Gと点G’は同じ点となります。従って、三角形の中線は1点で交わるということが証明できました。
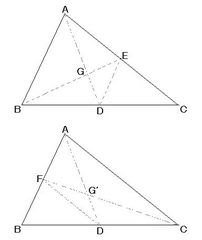
▲三角形の中線が1点で交わることの証明
図形(幾何学)好きの方は、残りの四心についても考えてみてください。
朝TVでは昨日より寒さが和らぐと言っていましたが、今日も充分寒いです。
中1の数学の授業で、「三角形の五心」を勉強しているということで、塾生とそれらの作図をしました。五心のうちの内心、外心、重心は、高校の数学Aで扱うので、中学の教科書には載っていませんが、きっと幾何学好きの先生なのでしょう。
五心のなかでも重心は身近な存在で、三角形の板を指の先にのせてバランスを取ると、その指の先が重心の位置になります。これは三角形に限ったことではなく、均質な板で作った任意の図形にあてはまることです。
三角形の重心の作図による求め方は、各頂点と対辺の中点を結ぶと3本の直線(中線といいます)が1点で交わり、この点を重心と言います。
また、重心は3本の中線を2:1に内分します。これは、直線上にない3つの同じ重さの錘を考えた場合、2つの錘の重心はそれらの中点で重さは2倍になります(「やじろべえ」です)。次に、それと残りの錘の重心を考えると、重心の位置はそれらを結んだ線分上にありますが、重さの比が2:1なので、その線分を1:2に内分する点になるということです。
ところで、最初に戻って「中線が1点で交わる」ということを証明するのは慣れていないと難しいかもしれません。と言うのは、中学校で勉強する図形の証明では、辺の長さや角の大きさが等しいことの証明などが多く、直線が1点で交わることの証明や3点が直線上にあることの証明などにお目にかかることはありません。
そこで、一例として三角形の中線が1点で交わることの証明を簡単に紹介します。
下図で点D、Eはそれぞれ辺BC、CAの中点で、ADとBEとの交点をGとします。そこで、DEを結ぶと、中点連結定理により、AB//EDで、AB:ED=2:1です。また、△GAB∽△GDEなので、BEはADを2:1に内分する点Gで交わります。
同様に、辺ABの中点Fとして、ADとCFとの交点をG’とすると、△G’AC∽△G’DFとなるので、CFはADを2:1に内分する点G’で交わります。
つまり、点Gも点G’もADを2:1に内分する点なので点Gと点G’は同じ点となります。従って、三角形の中線は1点で交わるということが証明できました。

▲三角形の中線が1点で交わることの証明
図形(幾何学)好きの方は、残りの四心についても考えてみてください。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます