本日は、無償学習塾の学習指導に参加しました。中学3年生の生徒さんに、理科の「力の合成」を解説しました。
合力
2つ以上の力がはたらいているとき、これらを1つの力に合わせたものを合力といいます。
力の合成
合力を求めることを力の合成といいます。
2つの力がはたらいており、これらの作用点が同じ位置であるとします。2つの力をF1,F2として、力を矢印で表記します。矢印の長さは力の大きさ、矢印の向きは力の向きを意味します。2つの力が一直線上にない場合は、下の図のように、F1,F2を2辺とする平行四辺形を考えます。
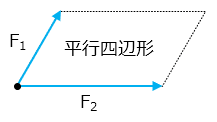
この平行四辺形の対角線が、F1,F2の合力Fになります。
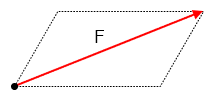
(別の考え方)
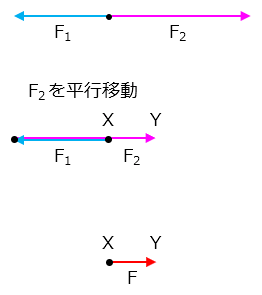
力の合成を考える場合に限り、力の矢印を平行移動して考えることができます。このとき、矢印の長さや向きを変えないように注意します。
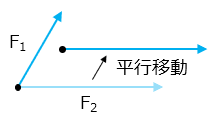
ある矢印の始点が、他の矢印の終点に重なるように矢印を平行移動します。例えば、F2の始点がF1の終点に重なるようにF2を平行移動すると、針金のように折れ曲がった1本の矢印になります。
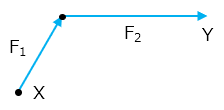
1本になった矢印の始点Xと終点Yを結んだ矢印が、F1,F2の合力Fになります。

2つの力F1,F2が一直線上にある場合も、同様にして合力Fを求めることができます。
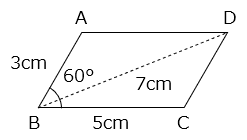
下の図のように,平行四辺形ABCDについて AB=3cm,BC=5cm,∠ABC=60°であるとき、対角線の長さは7cmになります。
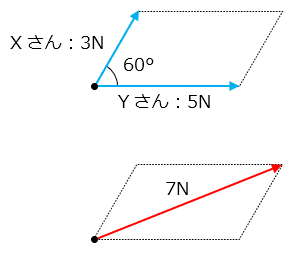
このことから、下の図のように、Xさんが3N,Yさんが5Nの力で、2力の間の角度が60°となるようにロープを引っ張ったとき、これらの合力は7Nになります。一人で赤矢印の向きに7Nの力でロープを引っ張っても、これと同等の状態になるといえます。
力の合成は、作図の問題として出題される場合もあります。本日の生徒さんは、平行四辺形の性質を活用し、着実に作図することができました。
合力
2つ以上の力がはたらいているとき、これらを1つの力に合わせたものを合力といいます。
力の合成
合力を求めることを力の合成といいます。
2つの力がはたらいており、これらの作用点が同じ位置であるとします。2つの力をF1,F2として、力を矢印で表記します。矢印の長さは力の大きさ、矢印の向きは力の向きを意味します。2つの力が一直線上にない場合は、下の図のように、F1,F2を2辺とする平行四辺形を考えます。

この平行四辺形の対角線が、F1,F2の合力Fになります。

(別の考え方)
力の合成を考える場合に限り、力の矢印を平行移動して考えることができます。このとき、矢印の長さや向きを変えないように注意します。

ある矢印の始点が、他の矢印の終点に重なるように矢印を平行移動します。例えば、F2の始点がF1の終点に重なるようにF2を平行移動すると、針金のように折れ曲がった1本の矢印になります。

1本になった矢印の始点Xと終点Yを結んだ矢印が、F1,F2の合力Fになります。

2つの力F1,F2が一直線上にある場合も、同様にして合力Fを求めることができます。

下の図のように,平行四辺形ABCDについて AB=3cm,BC=5cm,∠ABC=60°であるとき、対角線の長さは7cmになります。

このことから、下の図のように、Xさんが3N,Yさんが5Nの力で、2力の間の角度が60°となるようにロープを引っ張ったとき、これらの合力は7Nになります。一人で赤矢印の向きに7Nの力でロープを引っ張っても、これと同等の状態になるといえます。

力の合成は、作図の問題として出題される場合もあります。本日の生徒さんは、平行四辺形の性質を活用し、着実に作図することができました。









