等角螺旋が対数螺旋と呼ばれるのは（その１）

ブログ仲間のSUBALさんが久しぶりに黄金比について取り上げた記事を読み、リンクされている「自然の中の黄金比」を読み返して、昔から疑問に思っていたことを思い出しました。それは対数螺旋が等角螺旋と呼ばれる理由です。同じことですが、等角螺旋が対数螺旋なのは何故か、です。
これだけならば単に初等的な数学の問題ですが、対数螺旋の典型とされるオウムガイを引き合いに出してトンデモさん達がいい加減なことを振りまいているのが現状です。

生物界における形態を定量的に扱って生物物理の先駆者と看做されているのはダーシー・トムソンです。彼の著作"On Growth and Form"は1917年に初版が出ていますが、この分野では古典と言って良いと思います。同書は今でもペーパーバックで簡単に入手できますが、邦訳（抄訳）『生物のかたち』（東大出版会、初版1973年）は入手困難です。ともあれこのトムソンの著作を見ていくことにしましょう。
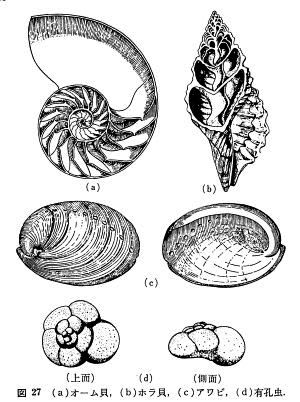
オウムガイ・ホラガイ・アワビ・有孔虫が図版で示され、この螺旋の歴史を簡潔に説明してくれます。邦訳101ページ。

「等角らせんはデカルトによって発見され，1638年のメルセンヌヘの手紙の中に述べられている．デカルトは，半径ベクトルと一定の角度で交わりながら成長する曲線の概念から出発し，半径ベクトルの長さはひと巻きごとに一定の比を保っていること，また，らせんによって切りとられる線分の長さもひと巻きごとに一定の比率で増大すること，

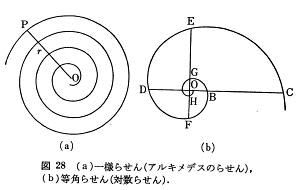
さらに図２８(b）に示すように，極Ｏから曲線上の任意の点Ｂ,Ｃまで曲線に沿って測った距離は，直線ＯＢ,ＯＣに比例することを説明した．
また，極Ｏを通る任意の２直線によって切りとられる曲線の部分はおのおの相似であり，そのために，この曲線はかたちを変えないで絶えず成長しているようにみえるということも示した．」

マラン・メルセンヌは僧侶でありながら科学に関心を持ち、当時のヨーロッパの学者をまとめる役割を果たしていました。当時の学者達は彼に成果を書簡で書き送ることが「学会発表」となったのです。デカルトがメルセンヌに研究成果を書き送った1638年はガリレオ・ガリレイが『新科学対話』をオランダで出版した年でもあります。日本では島原の乱が鎮圧されて天草四郎が処刑されました。

デカルトによるこの螺旋の定義から、まず等角螺旋として研究されたことが分かります。この螺旋を対数螺旋として研究したのはヤコブ・ベルヌーイです。この曲線は極形式で
ｒ＝a^θ
と表せます。両辺の自然対数をとって整理すると
θ＝log r/log a
aは定数だから、log aも定数で1/log a をkとすると
θ＝k log r
と表すことが出来ます。つまり「極のまわりの回転角は半径の対数に比例する」このことから，等角螺旋は対数螺旋とも呼ばれるのです。彼はこの螺旋が大変気に入って墓碑銘にこの螺旋を刻むように遺言したのですが、刻まれたのはアルキメデス螺旋だという話は有名です。

次回は対数螺旋の動径と接線のなす角度がθに関わりなく一定であることの初等的な証明を書きたいと思っています。

　　↓ポチッと応援お願いします！