Lフワ

LEDをじわーっと明るくすることをLフワと言うらしいのですが、Lチカに比べてちょっとコツがあります。

まず、LフワのためにPWM出力を利用します。

デューティを0から255まで増加させます。

しかし、これを実際に見るとじわーっと変化しないのです。

これは、人間の感覚が対数に比例しているからなのです。
このグラフの対数を見るとわかりやすいかと思います。

急に明るくなって変化が小さくなっていますね。

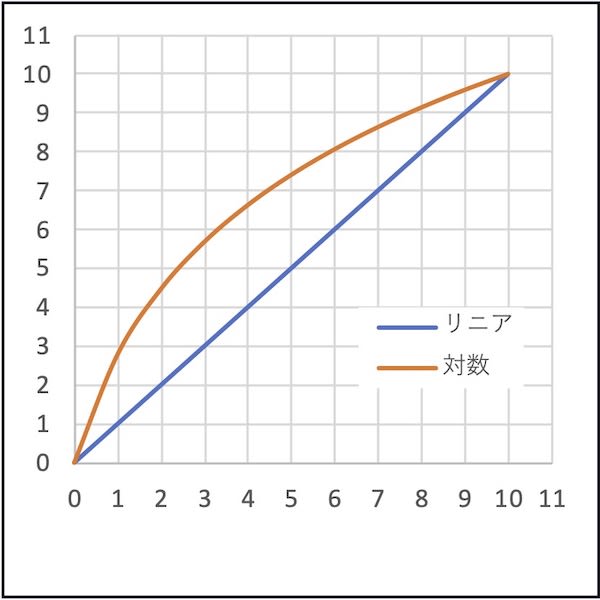
また、このグラフからデューティを50%にしても明るさは7割程度にしかならない。

明るさを半分にするにはデューティを30%くらいにしなければいけない。

と言うこともわかりますね。

（対数はLog 1が0なので、そこが原点になるようにずらして描いてます。式は後述）

と言うことはじわーっとリニアに光るようにするにはPWMを対数の逆関数の指数関数で増やせばいいことになります。

しかし、組み込みでは容量の小さな8ビットマイコンだったりするので指数関数を使うのは処理が重いです。

あらかじめ計算したデータを配列に置く方法だと、滑らかに変化させようとするとデータを細かくしてたくさん必要になって容量を圧迫します。

そこで、組み込みの世界では指数関数の代わりに二次関数を使います。


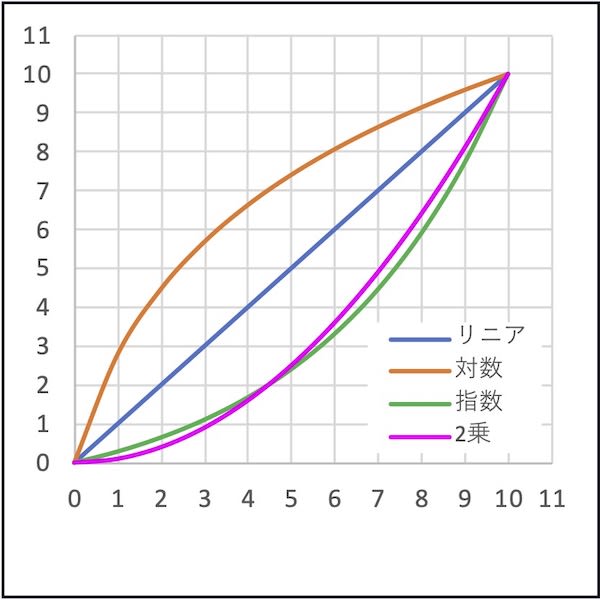
このグラフを見てください。

どうです？

２乗のグラフがほとんど指数関数に近いのが分かると思います。

２乗するだけなら容量も必要としませんし8ビットマイコンの整数演算でも速く処理できます。

ただしオーバーフローには注意してくださいね。


ATtiny402のフェードインスケッチ
http://ikkei.akiba.coocan.jp/ikkei_Electronics/ATtiny402.html

はこのようにして書いています。変化の時間やタイミングを簡単に変えられるようにconstrain()やmap()などのArduinoの関数をうまく利用しています。
興味のある人はコードを解析してみてください。


グラフの式
リニア　y = x
対数　　y = log( 1 + 0.9x) * 10
指数　　y = (10^(x/10) – 1) / 0.9
２乗　　y = x*x