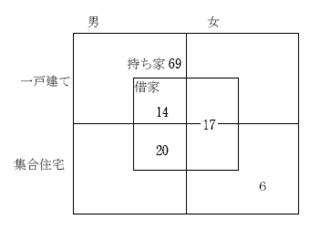
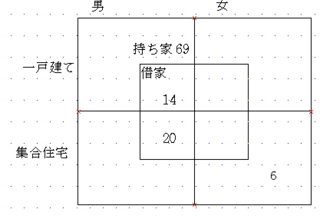
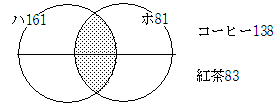
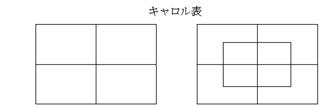
■ キャロル表
集合人数の問題では、問題によって、ベン図よりも別の書き方をしたほうがわかりやすい場合がある。
たとえば、でてくるものが大人と子供、女性と男性、日本人と外国人のように「対」あるいは「対等」になったものの場合、ベン図だと内側と外側になり把握しにくいことがある。「対等」な扱い、「対」の概念によって表される集合の場合には《キャロル表》と呼ばれる書き方をしてみるとよい。
(「キャロル表」という名称については、野崎昭弘「数学的センス」27ページ参照)
主と従 → ベン図

対等 → キャロル表
[問題]
ある会社の社員数は、男性30人、女性20人である。全員がパソコンを1台ずつ所有しており、それはデスクトップ型かノート型のどちらかである。デスクトップ型パソコンを所有している者は28人で、そのうち17人は男性である。また、インターネットを利用しているものは32人で、そのうち15人はノート型パソコンを所有している。インターネットを利用していない者のうち、8人は男性であり、5人はデスクトップ型パソコンを所有している女性である。このとき、ノート型パソコンを所有している男性でインターネットを利用している者は何人いるか。
1 10人
2 11人
3 12人
4 13人
5 14人
【解説】
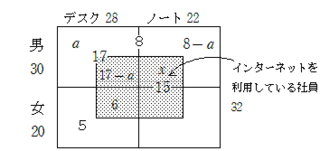
下のようなキャロル表を用意する。デスクトップ型パソコンを所有している男性でインターネットを利用していない者の人数をaとすると、デスクトップ型パソコンを所有していてインターネットを利用している男性は17-a人、ノート型パソコンを所有していてインターネットを利用していない男性は8-a人と表せる。
デスクトップ型パソコンを所有している28人のうち、てインターネットを利用している女性は、28-17-5=6 (人)。
インターネットを利用している社員の総数は32人だから、
(17-a)+6+15=32 ∴ a=6

求めるノート型でインターネットを利用している男性をx人とすると、男性の総数が30なので、6+11+x+2=30 となり、これを解いて、x=11(人)となる。
正答 2
掲載内容の無断転載、転用、編集を禁じます。