平面図形の分割構成 正六角形を分割

正六角形を８つの合同な図形に分けたとき，その１つであるのは，つぎのうちどれか．

　　　　　　　　　　　　

　　
















































　　　　　　　　　　　　　　　　　　　　　　　　　　　　正答　５

五角形を並べる 将棋の駒

　図１のような五角形がある。この五角形を図２のように配置すると一直線状に並ぶが，図３のように配置すると環状になる。五角形を図３のように環状に並べたとき，１周するためには図１の五角形が何枚必要になるか。



１　48枚
２　60枚
３　72枚
４　84枚
５　96枚















　　正答　３

直角二等辺三角形10枚で正方形

　図は，直角二等辺三角形10枚を組み合わせて作った図形である。この図形を，三角形の頂点を結ぶ直線分で切断して並べ替え，正方形を作りたい。切断する直線分を正しく示した図はどれか。

円、三平方の定理 解 その２

解　その２

△ＡＢＣと△ＡＨＢはともに、３：４：５の直角三角形。

したがって、ＢＡ：ＨＢ＝ＣＡ：ＢＣ
　　　　　　　　　　　＝10：８

　　　　　　ＨＢ＝ＢＡ×8/10＝4.8

　　　　　　　　　　　　　　　正答　３


　　　　　　

25枚の正方形 市松模様

　図Ⅰのように白黒の正方形の紙片を、四隅が黒となるように市松模様に並べて大きな25枚の正方形にする。
　図ⅡのＡ～Ｇのような正方形をつなげた紙片で図Ⅰを埋めつくすとき、必要のない紙片のみを挙げているものはどれか。
　ただし、Ａ～Ｇは裏返して使用することはないものとする。なお、アの紙片がすでに１枚置かれている。


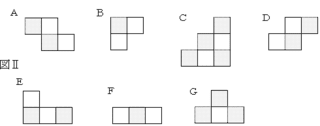
　１　Ａ、Ｃ
　２　Ａ、Ｄ
　３　Ｂ、Ｅ
　４　Ｅ、Ｇ
　５　Ｄ、Ｆ

　　






【ヒント】市松模様の利用






【解説】
　□の面積を１とする。面積と模様の黒白の個数を利用する。

　図Ⅰを埋め尽くすには面積20分(黒10、白10)が必要で、Ａ～Ｇの面積の合計が28(黒15、白13)なので、面積８(黒５、白３)だけ余分。

　選択肢１～５の中で面積が８であるのは、２ Ａ、Ｄと４ Ｅ、Ｇ。



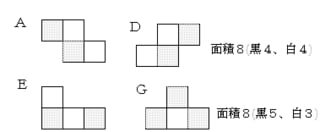
　よって、黒白の個数を考慮に入れると、必要のない紙片はＥとＧ。

　実際、Ａ、Ｂ、Ｃ、Ｄ、Ｆを用いて次のように埋め尽くすことができる。


　　　　 　　　　　　　　　　正答　４

掲載内容の無断転載、転用、編集を禁じます。

正多角形による床の敷き詰め

　合同な正多角形のタイル１種類を用いて、すき間のないように床に貼っていきたい。下のア～エのうちから、すき間のないように貼れるタイルの形を２つ選んだ組合せとして正しいものはどれか。
　ただし、床の端にすき間ができるのは差し支えないものとする。
　ア　正三角形　　　イ　正五角形　　
　ウ　正六角形　　　エ　正八角形
１　ア、イ
２　ア、ウ
３　ア、エ
４　イ、ウ
５　イ、エ











【解説】
　正多角形のタイルで床をすき間なしに貼るためには、正多角形の内角が、360°を割り切ることが条件。
　ア～エの正多角形の内角を求めてみる。

　一般に正ｎ角形の内角を求めるやり方は次の２通りがよく知られている。
① 正ｎ角形の内角の総和を求めてｎで割る。
② 正ｎ角形の外角を求めて180°から引く。

　ここでは②のやり方で求めてみる。多角形の外角の総和はいつでも360°であり、正多角形の場合すべての外角は等しい。
　ア 正三角形
　　　　外角　360°/３＝120°、内角 180°－120°＝60°
　イ 正五角形
　　　　外角　360°/５＝72°、内角 180°－72°＝108°
　ウ 正六角形
　　　　外角　360°/６＝60°、内角 180°－60°＝120°
　エ 正八角形
　　　　外角　360°/８＝45°、内角 180°－45°＝135°

　これらのうちで360°を割り切るのは、アの60°とウの120°。　　　　　　　　　　　　　　　　　　　　　　　　　　　　正答　２