楽天的な人 解説

Ａは通常、ベン図で図Ⅰのように表せる。
しかし、Ｄの対偶「￢音 → 楽」(図Ⅱ)より、図Ⅲのようになり、結局主張していることは「国 → 楽」と同じことになる。



　ＡとＤ：国 → 楽
　Ｂ： 理 → 国
　Ｃ：　　楽 → 体
　Ｅ：　　￢理 → 数　　対偶　数 → 理
　Ｆ：　　体 → ロ

これらをまとめると、
　　　　　数 → 理 → 国 → 楽 → 体 → ロ

この対偶は
　　　　　￢ロ → ￢体 → ￢楽 → ￢国 → ￢理 → ￢数

　選択肢３「ロマンチストでない人は数学が得意でない」が正しい。

　　　　　　　　　　　　　　　　　　　正答　３

楽天的な人

　科目の得意、不得意と性格との関係を調べたところ、次のＡ～Ｆのことがわかった。このとき、確実にいえるのはどれか。
　Ａ：国語が得意な人は音楽が得意でないか、又は楽天的だ。
　Ｂ：理屈っぽい人は国語が得意だ。
　Ｃ：楽天的な人は英語が得意だ。
　Ｄ：楽天的でない人は音楽が得意だ。
　Ｅ：理屈っぽくない人は数学が得意でない。
　Ｆ：英語が得意な人はロマンチストだ。
　１　国語が得意な人は数学も得意だ。
　２　理屈っぽい人は英語が得意でない。
　３　ロマンチストでない人は数学が得意でない。
　４　楽天的な人は理屈っぽくない。
　５　英語が得意な人は国語も得意だ。

判断推理

知能問題 標準判断推理

上・中級公務員 標準判断推理―確かな解答力が身につく“基本書” 実務教育出版 このアイテムの詳細を見る

　

チェスのナイト

　チェスのナイトは図Ⅰのように動くことができる。このとき図ⅡのＡから動かし始めて奇数回で到達できるのはa～eのうちどれか。

１　a　　　　
２　b　　　　
３　c　　　　
４　d　　　　
５　e　

メビウスの輪

　図Ⅰのような中心に点線が１本入った長さＬのテープがある。この紙テープの両端を半回転(180°)ひねってつなぎ、輪にした。テープの両端に注目すると図Ⅱのように○の端と×の端がつながっているので、紙テープの点線に沿って切ると、長さ２Ｌのねじれた１つの輪ができることがわかる。図Ⅲのような点線が４本入った長さＬの紙テープの両端を半回転ひねってつなぎ、点線をすべて切るとどのようになるか。

１　長さ５Ｌの輪が１つできる。
２　長さＬの輪が１つと長さ４Ｌの輪が１つできる。
３　長さＬの輪が２つと長さ３Ｌの輪が１つできる。
４　長さＬの輪が１つと長さ２Ｌの輪が２つできる。
５　長さＬの輪が３つと長さ２Ｌの輪が１つできる。

虫食い算 かけ算

　次の式はあるかけ算の筆算であるが、数字が７か８のいずれかであれば□、その他の数字は＊で表されている。
　このとき、このかけ算の結果はいくらか。
　　　　　　　　＊ ＊
　　　　　×　　＊ ＊
　　　　　－－－－－－－
　　　　　　　　＊ ＊
　　　　　　 ＊ □
　　　　　－－－－－－－
　　　　　　 □ ＊ ＊
１　714
２　734
３　756
４　834
５　856

長方形と正方形 針金

　同じ長さの針金２本をそれぞれ曲げて長方形と正方形を作り、面積を比べたところ、３：４になったという。この場合、長方形の縦横の２辺の比はいくらになるか。ただし、長方形は縦のほうが横よりも長いものとする。
１　２：１
２　３：１
３　５：２
４　７：２
５　８：３

４ケタの整数 ９で割り切れるとき 解説

【解説】
　Ａが９で割り切れるためには、ａ＋ｂ＋ｃ＋ｄ、すなわち各位の数字の和が９の倍数であることが条件である。

７＋□＋６＋□が９の倍数になるのは、２つの□内の数字の和が５だと18に、14だと27になり、９の倍数であるといえる。

　２つの□内の数字の和は、５または14

　　　　　　　　　　　　　　　正答　５

4ケタの正の整数 ９で割り切れるとき

　４桁の正の整数Ａ＝1000ａ＋100ｂ＋10ｃ＋ｄは、Ａ＝９(111ａ＋11ｂ＋ｃ)＋(ａ＋ｂ＋ｃ＋ｄ) と表せる。これを利用し、４桁の数７□６□が９で割り切れるときに、□に入る２つの数字の和はいくつか。
１　４のみ　　　
２　５のみ　　　
３　６のみ　　　
４　４または13
５　５または14

 

 

 

 

• 
• 
• 
• 

a,b,c,d の正負 数的推理

　実数a,b,c,d について
　　a＋b＜０、c＋d＜０、abcd＜０
が成り立っているとき、a,b,c,d の正負についての記述として正しいものは、次のうちどれか。
１　正の数が必ず１つだけある。
２　正の数が必ず２つだけある。
３　正の数が必ず３つだけある。
４　正の数が１つの場合と２つの場合がある。
５　正の数が１つの場合と３つの場合がある。

正二十面体について 解説

　正二十面体では、1つの頂点に５つの面が集まっている。

　展開図の中で5つの面が集まっている頂点に注目し、辺を閉じ合わせていく。

　白丸○の頂点は5つの面が集まっているので、開いている部分は閉じ合わさる。

　そのことによって、たとえばＰとＱは重なり、頂点Ｐ(＝Ｑ)に集まる５つの面が確定するので、開いている辺ＰＲとＱＳが合わさる。その結果、ＲとＳが重なることになる。

　これを続けていくと、ＴとＥ、ＰとＤが重なることが分かる。



　点Ｐは点Ｄと重なる。

　また、ＰはＵ、Ｗとも重なることも同様にしていえる。

　　　　　　　　　　　　　　　　　　　　　正答　４

正二十面体について

　次の図は正二十面体の展開図であるが、図中の点Ａ～Ｅのうち、組み立てたとき点Ｐと重なるのはどれか。

１　Ａ　　　
２　Ｂ　　　
３　Ｃ　　　
４　Ｄ　　　
５　Ｅ

正十二面体について

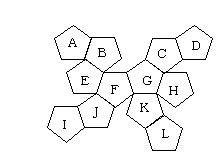
　次の図は、各面にＡ～Ｌの文字をつけた正十二面体の展開図である。この展開図を組み立てたとき、互いに平行になる面の組合せとして正しいものはどれか。

１　ＡとＨ
２　ＢとＬ
３　ＣとＩ
４　ＤとＫ
５　ＥとＣ



知能問題 標準判断推理

上・中級公務員 標準判断推理―確かな解答力が身につく“基本書” 実務教育出版 このアイテムの詳細を見る