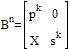予備校＆塾の講師

予備校または塾の正社員の数学の講師をしたいと思っています。

PM5:00-PM10:00 ぐらいの時間帯ではないでしょうか？
勤務地は、茨城県の土浦市・つくば市、電車で通える範囲（水戸など）が希望
なかなか、大卒などが多く自分の条件に合っていないところが多く、探すのに苦労しています。

城西大学・理学部・数学科（１年中退）
Skype ID:logicalspace

東大数学の難易度

ときどき、「東大数学の解き方」で訪れる方がいます。

まずは、難易度です。
2009年度の東大前期の理系数学の①～⑤の解答を掲載しました。
⑥もあるのですが、割愛を致します。

難易度は、標準問題の融合問題が多いということが特徴としてあげられます。
融合問題が多いということは、苦手な分野を作ると点数が取れないということです。
まんべんなく、どの分野の標準問題をこなして、融合問題に対応する準備が必要であります。

解き方は、標準問題を解けるようにすることです。
そうすると、東大前期の数学は解けると思います。
ときどき、難問が出題されますが、標準問題を解ければ、自然と解けるようになると思います。


なぜ、融合問題が多いのか？
大学の数学は、より抽象的な数学になります。
抽象的な数学は、考え方、具体的から抽象的へなど、広い視野が求められます。

例えば、ε－δ論法（解析学）、環（代数学）などがそうです。
ε－δ論法は、極限についてを厳密に取り扱う論法です。　大きい、小さいの概念が中途半端に考えているのかが分かります。
環は、計算法則についての定義からさまざまな定理を導きだしています。　５次方程式には一般解の公式が存在しないのも、環⇒体⇒ガロア理論より証明されています。
抽象数学を高校生にはそのまま出題が出来ないので、融合問題として出題していると思われます。
抽象数学が理解が出来れば、必ずしも解ける訳ではありませんが、基礎学力を問うには、融合問題が適していると思われます。
※ε－δ論法、環などは、高校の範囲を超えるので、今は知る必要はないです。

数学の家庭教師

数学の家庭教師をすることにしました。

対象は、小・中・高です。
家庭教師を経営する会社へと登録をしました。
もちろん、アルバイトです。

少しづつ、社会復帰をしないといけないので、体調が比較的によい夕方の仕事を探していたので、良かったです。

東大数学 前期(2009)_(5)

＜⑤の問題＞
(1) 実数 x が -1 ＜ x ＜ 1、x ≠ 0 をみたすとき、次の不等式を示せ。 (1-x)^1-1/x ＜ (1+x)^1/x
(2) 次の不等式を示せ。 0.9999¹⁰¹ ＜ 0.99 ＜ 0.9999¹⁰⁰


＜解答＞
(1)
両辺を対数をとる
(1-1/x)log(1-x) ＜ 1/x・log(1+x) ・・・①を示せばよい。

0 ＜ x ＜ 1 では、⇔ (x-1)log(1-x) ＜ log(1+x)
-1 ＜ x ＜ 0 では、⇔ (x-1)log(1-x) ＞ log(1+x)

f(x) = log(1+x) - (x-1)log(1-x)
f'(x) = 1/(x+1) - log(1-x) - (1-x)・(-1)/(1-x)
f'(x) = 1/(x+1) - log(1-x) - 1
f''(x) = -1/(x+1)² - (-1)/(1-x) = x(x+3)/(1+x)²(1-x)

f''(x) -1 ... (-) ... 0 ... (+) ... 1
f'(0) = 0 より f'(x) ≧ 0 (-1 ＜ x ＜ 1)
f(0) = 0 より、0 ＜ x ＜ 1 で f(x) ＞ 0, -1 ＜ x ＜ 0 でf(x) ＜ 0 となり、題意は示された。

(2)
(1-x)^1-1/x ＜ (1+x)^1/x ・・・②
②に x = 0.01 を代入、0.99^-0.99 ＜ 1.01¹⁰⁰
両辺を0.99¹⁰⁰倍して、0.99 ＜ 0.9999¹⁰⁰
②に x = -0.01 を代入、1.01¹⁰¹ ＜ 0.99^-100
両辺を0.99¹⁰¹倍して、0.9999¹⁰¹ ＜ 0.99


＜解説＞
不等式の証明には、簡単な式では、式変形や公式を使用して証明します。
複雑な式では、差または商より微分して増減表より証明します。

東大数学 前期(2009)_(4)

＜④の問題＞
a を正の実数とし、
空間内の２つの円板
D₁ = { (x, y, z) | x² + y² ≦ 1, z ＝ a},
D₂ = { (x, y, z) | x² + y² ≦ 1, z ＝ -a}
を考える。
D₁ を y 軸の回りに 180°回転して、D₂ に重ねる。
ただし、回転は z 軸の正の部分を x 軸の正の方向に傾ける向きとする。
この回転の間に D₁ が通る部分を E とする。
E の体積を V(a) とし、E と { (x, y, z) | x ≧ 0} との共通部分の体積を W(a) とする。

(1) W(a) を求めよ。
(2) lim_{a → ∞}V(a) を求めよ。


＜解答＞
(1)
平面 y = k (-1 ≦ k ≦ 1) による D₁ の切り口は、x² + k² ≦ 1, z = a より
180°回転させると、外の円は半径 1、内の円の半径 k² の間の部分となり
x ≧ 0 の部分の面積は、π/2・(1 - k²)


(2)
E の x ≦ 0 の部分の体積をU(a)、面積をS(k) とする。
半径 1 と半径 k² の差の部分を S(k) とする。
S(k) は、２つの孤の差の面積なので、そこの部分の長方形の T(k) を考える。
S(k) ≦ T(k) = 2√(1 - k²)(√(1 - k² + a²) - a) = 2√(1 - k²)(1 - k²) / (√(1 - k² + a²) + a) = 2(1 - k²)^3/2 / (√(1 - k² + a²) + a)
≦ 2(1 - k²)^3/2 / a = 2/a・(1 - k²)^3/2

・・・①
a → ∞ のとき、①の最右辺 → 0 だから、はさみうち原理より、U(a) → 0
∴ V(a) → W(a) = 2/3・π


＜解説＞
点の軌跡より、曲線を求める問題は多いと思います。
今回は、空間の面積の軌跡より体積を求める問題になります。
なので、軌跡の問題に慣れる必要があります。

また、(x, y, z) の空間をイメージする問題です。
求める体積は、面積を積分することを使っています。
さらに、(2) では、はさみうちの原理を使っています。

軌跡・空間・積分の融合問題なので、苦手な分野があると点数が取れないと思います。

東大数学 前期(2009)_(3)

＜③の問題＞
スイッチを１回押すごとに、赤、青、黄、白のいずれかの色の玉が１個、等確率1/4で出てくる機械がある。　２つの箱 L と R を用意する。　次の３種類の操作を考える。
（A）１回スイッチを押し、出てきた玉を L に入れる。
（B）１回スイッチを押し、出てきた玉を R に入れる。
（C）１回スイッチを押し、出てきた玉と同じ色の玉が、L になければその玉を L に入れ、L にあればその玉を R に入れる。

（１）L と R は空であるとする。　操作（A)を５回おこない、さらに操作（B）を５回おこなう。　このとき L も R にも４色すべての玉が入っている確率 P₁ を求めよ。
（２）L と R は空であるとする。　操作（C)を５回おこなう。　このとき L に４色すべて玉が入っている確率 P₂ を求めよ。
（３）L と R は空であるとする。　操作（C)を１０回おこなう。　このとき L にも R にも４色すべての玉が入っている確率 P₃ とする。　P₃/P₁ を求めよ。


＜解答＞
（１）
L に４色そろうのは、赤、青、黄、白のうちの１色が２回、他が各１回・・・①　出るとき。
どの色が２回かで４通り、赤赤青黄白の場合、これからの順序は5!/2!=5・4・3通り。
他の場合も同様で、L に４色そろう確率は、 4 × 5・4・3 / 4⁵ = 15/64 ・・・②
R に４色そろう確率も②と同じで、P₁ = ②²

（２）
L に４色そろうのは①の場合で、P₂ = ② = 15/64

（３）
L も R も４色そろうのは各色が２回以上出る場合で、どの色が何回でるかは、次の２タイプ：
１）２回、２回、２回、４回
２）２回、２回、３回、３回
１）のとき：どの色が４回かで４通り。
赤２回、青２回、黄２回、白４回の場合、赤、青、黄が何回目かは₁₀C₂・₈C₂・₆C₂ = 45・28・15通り。
他の場合も同様。
２）のとき：どの色が２回かで₄C₂=６通り、赤２回、青２回、黄３回、白３回の場合、赤、青、黄が何回目かは₁₀C₂・₈C₂・₆C₃ = 45・28・20通り。
他の場合も同様。
以上から、P₃ = (4 × 45・28・15 + 6 × 45・28・20) / 4¹⁰
また、P₁ = (4 × 5・4・3)² / 4¹⁰ だから
P₃/P₁ = (4 × 45・28・15 + 6 × 45・28・20) / (4 × 5・4・3)² = (7・3 + 6・7) / 4・4 = 63/16

東大数学 前期(2009)_(2)

＜②の問題＞
実数を成分にもつ行列 と実数r, s が下の条件 ()、()、() をみたすとする。
() s ＞ 1
()
(） (n = 1, 2, ...) とするとき、

このとき以下の問に答えよ。
(1) を a, c, r, s を用いて表せ。
(2) (n = 1, 2, ...) とするとき、
(3) c ＝ 0 かつ |a| ＜ 1 を示せ。


＜解答＞
(1)
、 より

∴

(2)
とおくと B = P^-1AP だから、

n → ∞ のとき、x_n → 0、y_n → 0 だから、z_n → 0、w_n → 0

(3)
a - cr = p とおくと

から、B²、B³ 計算して、Bⁿ を以下のように推測できる。

ただし、X = c(p^k + p^k-1s + ... + s^k)

数学的帰納法より証明をしますが、割愛をします。　（答案には証明を書く）


ただし、X = c(p^k + p^k-1s + ... + s^k)
(2) より、n → ∞ のとき、p^k → 0 ・・・①
よって、|p| ＜ 1、(） s ＞ 1 ・・・②
p ≠ s
∴w_n = c・(pⁿ - sⁿ) / (p - s)
①、②より、n → ∞ のとき、pⁿ - sⁿ → -∞ であり、w_n → 0 より c = 0
p = a - cr = a より p = a より |a| ＜ 1


＜解説＞
(1)
任意の行列 A に対して、、 この式が成り立つならば が成り立つ。

(2) B = P^-1AP ならば、Bⁿ = P^-1AⁿP が成り立つ。
(3) 式は複雑になるが、計算力の問題です。


＜ポイント＞
具体的な数値を扱う問題ではなく、行列、数列、極限の性質を利用した問題です。
また、行列、数列、極限の融合問題です。
なので、苦手な部分があると点数が取れません。

東大数学 前期(2009)_(1)

＜①の問題＞
自然数 m ≧ 2 に対し、m-1 個の二項係数_mC₁, _mC₂ , ... , _mC_m-1 を考え、これらすべての最大公約数を d_m とする。
すなわち、d_m はこれらすべてを割り切る最大の自然数である。

(1) m が素数ならば、d_m = m であることを示せ。
(2) すべての自然数 k に対し、k^m - k が d_m で割り切ることを、k に関する数学的帰納法によって示せ。
(3) m が偶数のとき、d_m は 1 または 2 であることを示せ。


＜解答＞
(1)
_mC₁ = m だから、_mC_i(i = 1, 2, ... , m-1) が m の倍数になることを示せばよい。
_mC_i = m(m-1) ... (m-(i-1)) / i(i-1) ... 1 = m・(m-1) ... (m-(i-1))/ i(i-1) ... 1 = m・X
(X = (m-1) ... (m-(i-1))/ i(i-1) ... 1 とおく)
i ≦ m-1 より、m が素数ならば、m と i, i-1, ... , 1 は、互いに素だから、X が約分されて整数となり、m の倍数。

(2)
k = 1 のとき、k^m - k = 0 は d_m の倍数
k = n のとき成り立つと仮定すると、n^m - n は d_m の倍数 ・・・①
k = n + 1 のとき、
(n + 1)^m - (n + 1)
= _nC₀n⁰ + _nC₁n¹ + ... + _nC_tn^t + ... + _nC_m-1n^m-1 + _nC_mn^m - (n + 1)
ただし、t は(n + 1)^m を展開したときの t項目です。
= 1 + _nC₁n¹ + ... + _nC_tn^t + ... + _nC_m-1n^m-1 + n^m - (n + 1)
= _nC₁n¹ + ... + _nC_tn^t + ... + _nC_m-1n^m-1 + n^m - n ・・・②

_nC_t (1 ≦ t ≦ m-1) は、d_m の倍数で、これと①より、②は d_m の倍数だから、k = n + 1 のときも成り立つ。
よって、題意は示された。

(3)
(2) より k^m - k ≡ 0 (mod d_m) (k ＝ 0 でも成立)
だから、k = d_m - 1 として
(d_m - 1)^m - (d_m - 1) ≡ 0 (mod d_m)
∴ (-1)^m + 1 ≡ 0
m は偶数だから、 2 ≡ 0 となり、2 は d_m の倍数。
よって、d_m は 1 または 2。


＜解説＞
n! = n(n-1)...2・1 ただし、1! = 0! = 1 と定義する
_nC_r = n! / r!(n-r)!
を教科書で確認する。

(a + b)ⁿ = _nC₀ + _nC₁a^n-1b + ... + _nC_ra^n-rb^r + ... + _nC_n-1ab^n-1 + _nC_nbⁿ
を教科書で確認する。

互いに素は、最大公約数が 1 であること。

数学的帰納法の証明を教科書より確認する。

n ≡ r (mod d) の合同式とは、n ÷ d = X あまり r を意味する。
商 X は扱わなく、剰余（あまり）r を扱うときに、使う記号です。
本来は、大学の代数学で習う記号です。　大学受験より、教える予備校もあります。　たぶん、進学校では教えると思います。
プログラムの BASIC をすると、mod の命令を使います。


＜ポイント＞
₅C₃ = 5! / 3!(5-3)! = 5! / 3!2! = 5・4 / 2・1 = 5・2 = 10
のように、具体的な数字を扱う訳ではないということです。
変数を用いて、数学的な性質を取り扱っていること。

(1) _mC_i = m・X というに、_mC_i が、m の倍数であることの性質を見抜くこと。
m が素数であれば、m とm以外は、必ず互いに素であること。

(2) (n + 1)^m - (n + 1) = = _nC₁n¹ + ... + _nC_tn^t + ... + _nC_m-1n^m-1 + n^m - n と変形をすること。