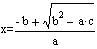===== 数学A・Ⅰ =====
(2次方程式の解の公式)
ax
2 + bx + c = 0


ax
2 + 2bx + c = 0 (b ⇒ 2bの場合)
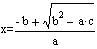

(2次方程式の実数解の個数)
ax
2 + bx + c = 0 の判別式 D とすると
D = b
2 - 4ac > 0 ⇔ 異なる2つの実数解をもつ
D = b
2 - 4ac = 0 ⇔ ただ1つの実数解(重解)をもつ
D = b
2 - 4ac < 0 ⇔ 実数解を持たない。(異なる2つの複素数解をもつ)
※重解は正しい表現ではありません。 正しくは重根が正しいです。 大学の代数学入門で教えてもらうので、気にすることはありません。
(解と係数の関係)
ax
2 + bx + c = 0 の2つの解をα、βとすると
α + β = - b / a、α・β = c / a
(2次式の因数分解)
ax
2 + bx + c = 0 の2つの解をα、βとすると
ax
2 + bx + c = a(x - α)(x - β)
とくに、重解αをもつとき
ax
2 + bx + c = a(x - α)
2
(補足)
3次方程式、4次方程式の解の公式は存在します。
5次方程式以上は、解の公式は存在しません。 数学者のガロアが公式がないことを証明しています。
ただし、5次方程式の解は、超越関数を使うと公式はあるようですが・・・。
もちろん、n次方程式の「判別式」と「解の係数と関係」もあります。
これは、代数学入門でならいます。