＜②の問題＞
実数を成分にもつ行列
と実数r, s が下の条件 ()、()、() をみたすとする。
() s ＞ 1
()
(）
(n = 1, 2, ...) とするとき、
このとき以下の問に答えよ。
(1)
を a, c, r, s を用いて表せ。
(2)
(n = 1, 2, ...) とするとき、
(3) c ＝ 0 かつ |a| ＜ 1 を示せ。
＜解答＞
(1)
、
より
∴
(2)
とおくと B = P-1AP だから、
n → ∞ のとき、xn → 0、yn → 0 だから、zn → 0、wn → 0
(3)
a - cr = p とおくと
から、B2、B3 計算して、Bn を以下のように推測できる。
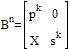
ただし、X = c(pk + pk-1s + ... + sk)
数学的帰納法より証明をしますが、割愛をします。 （答案には証明を書く）
ただし、X = c(pk + pk-1s + ... + sk)
(2) より、n → ∞ のとき、pk → 0 ・・・①
よって、|p| ＜ 1、(） s ＞ 1 ・・・②
p ≠ s
∴wn = c・(pn - sn) / (p - s)
①、②より、n → ∞ のとき、pn - sn → -∞ であり、wn → 0 より c = 0
p = a - cr = a より p = a より |a| ＜ 1
＜解説＞
(1)
任意の行列 A に対して、
、
この式が成り立つならば 
が成り立つ。
(2) B = P-1AP ならば、Bn = P-1AnP が成り立つ。
(3) 式は複雑になるが、計算力の問題です。
＜ポイント＞
具体的な数値を扱う問題ではなく、行列、数列、極限の性質を利用した問題です。
また、行列、数列、極限の融合問題です。
なので、苦手な部分があると点数が取れません。
実数を成分にもつ行列
と実数r, s が下の条件 ()、()、() をみたすとする。() s ＞ 1
()
(）
(n = 1, 2, ...) とするとき、このとき以下の問に答えよ。
(1)
を a, c, r, s を用いて表せ。(2)
(n = 1, 2, ...) とするとき、(3) c ＝ 0 かつ |a| ＜ 1 を示せ。
＜解答＞
(1)
、 より∴
(2)
とおくと B = P-1AP だから、n → ∞ のとき、xn → 0、yn → 0 だから、zn → 0、wn → 0
(3)
a - cr = p とおくと
から、B2、B3 計算して、Bn を以下のように推測できる。
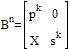
ただし、X = c(pk + pk-1s + ... + sk)
数学的帰納法より証明をしますが、割愛をします。 （答案には証明を書く）
ただし、X = c(pk + pk-1s + ... + sk)
(2) より、n → ∞ のとき、pk → 0 ・・・①
よって、|p| ＜ 1、(） s ＞ 1 ・・・②
p ≠ s
∴wn = c・(pn - sn) / (p - s)
①、②より、n → ∞ のとき、pn - sn → -∞ であり、wn → 0 より c = 0
p = a - cr = a より p = a より |a| ＜ 1
＜解説＞
(1)
任意の行列 A に対して、
、 この式が成り立つならば が成り立つ。(2) B = P-1AP ならば、Bn = P-1AnP が成り立つ。
(3) 式は複雑になるが、計算力の問題です。
＜ポイント＞
具体的な数値を扱う問題ではなく、行列、数列、極限の性質を利用した問題です。
また、行列、数列、極限の融合問題です。
なので、苦手な部分があると点数が取れません。