6月3日(火)~14日(土)の期間は、急性胆のう炎で入院していました。
来月の4月から消費税増税になります。
現在の5%の消費税の金額が、y 円ならば、消費税抜きは、y ÷ 1.05 = y ÷ (105 / 100) = y × (100 / 105)
4月からの8%の消費税の金額は、y × (100 / 105) × 1.08 = y × (100 / 105) × (108 / 100) = y × (108 / 105)
= y × {(105 + 3) / 105} = y × (1 + 3 / 105)
実際に、5%の表示価格から8%の表示価格の差額は、y × (1 + 3 / 105) - y = 3y / 105 = y / 35
5%の表示価格から8%の表示価格の差額を、x 円とします。
y / 35 = x ⇔ y = 35x
y 円が3500 ~ 7000円 では、x 円が100 ~ 200円増しです。
y 円が35000 ~ 70000円は、x 円が1000~ 2000円増しです。
明けましておめでとうございます。
去年の12月上旬から急に忙しくなり、更新が遅れています。
今年も更新は遅れますが、ブログをよろしくお願い致します。
※時間がある時に、コメントは読んでいますよ。
相棒で、数学をテーマにした架空の事件でした。
でも、どこが架空で、どこが本当なのか?
真実と架空が少し混ざっている内容でした。
証明に「背理法」はあります。
しかし、背理法の使い方が間違っています。
ファーガスの定理は、架空の定理なので、存在はしません。
しかし、ミレニアム問題が7つあり、賞金100ドルが懸ってあることは、本当です。
リーマン予想が約150年間が未解決問題というのは、本当です。
また、リーマン予想と素数が関係がしていることは、本当です。
大きな素数、πなどの無理数が、暗証鍵に使われていることは、本当です。
「みんなの数学」という雑誌はありません。
「数学セミナー」という雑誌は本当にあります。
ファイルの一番右にファーガスの定理がありませんでした。
右京さんが左からファイルを読みました。
ファーガスの定理以外は、本当にある数学の分野です。
「ABC予想」も本当に、最近の京大の教授が予想しまして、現在、検証されている予想です。
教授の部屋に行って、透明なガラスにグラフが書かれていました。
あのグラフは、楕円関数論に出てくるグラフです。
素数が、数学の元素と言われていることは、本当です。
数学者で素数の研究をしているのは、本当ですが、色々な分野との関わりの中で研究していので、素数を単独で研究はしていないと思います。
普通に相棒を見たかったですが、至る所に数学関係の話があるので、奇妙な気分でドラマを見ました。
でも、どこが架空で、どこが本当なのか?
真実と架空が少し混ざっている内容でした。
証明に「背理法」はあります。
しかし、背理法の使い方が間違っています。
ファーガスの定理は、架空の定理なので、存在はしません。
しかし、ミレニアム問題が7つあり、賞金100ドルが懸ってあることは、本当です。
リーマン予想が約150年間が未解決問題というのは、本当です。
また、リーマン予想と素数が関係がしていることは、本当です。
大きな素数、πなどの無理数が、暗証鍵に使われていることは、本当です。
「みんなの数学」という雑誌はありません。
「数学セミナー」という雑誌は本当にあります。
ファイルの一番右にファーガスの定理がありませんでした。
右京さんが左からファイルを読みました。
ファーガスの定理以外は、本当にある数学の分野です。
「ABC予想」も本当に、最近の京大の教授が予想しまして、現在、検証されている予想です。
教授の部屋に行って、透明なガラスにグラフが書かれていました。
あのグラフは、楕円関数論に出てくるグラフです。
素数が、数学の元素と言われていることは、本当です。
数学者で素数の研究をしているのは、本当ですが、色々な分野との関わりの中で研究していので、素数を単独で研究はしていないと思います。
普通に相棒を見たかったですが、至る所に数学関係の話があるので、奇妙な気分でドラマを見ました。
【数学者】
「仕事をしているのに、ハタ目からはボーッとしてるようにしか見られない」(某国立大学数学科准教授Sさん)というのは数学者共通の悩み。
やはり素数が好きな人は多くて、
「傘立てや居酒屋の下駄箱は素数の番号を選ぶ」(同Oさん)、
「車で走ってるとき国道の番号が素数だとうれしい」(Sさん)とか。
「紙ナプキンや箸袋に思いついた数式を書いたりすることがある。なので、胸ポケットには常にペンが入っている」(同)ってのは、わからなくはないが、
「酒の席でルベーグとフーリエ(ともに有名な数学者)のどっちが偉いかという話で盛り上がる」(Oさん)となると一般人には理解不能だ。
Yahooより
「仕事をしているのに、ハタ目からはボーッとしてるようにしか見られない」(某国立大学数学科准教授Sさん)というのは数学者共通の悩み。
やはり素数が好きな人は多くて、
「傘立てや居酒屋の下駄箱は素数の番号を選ぶ」(同Oさん)、
「車で走ってるとき国道の番号が素数だとうれしい」(Sさん)とか。
「紙ナプキンや箸袋に思いついた数式を書いたりすることがある。なので、胸ポケットには常にペンが入っている」(同)ってのは、わからなくはないが、
「酒の席でルベーグとフーリエ(ともに有名な数学者)のどっちが偉いかという話で盛り上がる」(Oさん)となると一般人には理解不能だ。
Yahooより
(1) P(1) が成り立つ
(2) ∀k [P(k) ⇒ P(k+1)] が成り立つ
∀の n のP(n) 成り立つ
論理記号学で書くと、上記のようになります。
私は、[∀k P(k) ⇒ ∀k P(k+1)] と勘違いしていました。
(2) ∀k [P(k) ⇒ P(k+1)] が成り立つ
∀の n のP(n) 成り立つ
論理記号学で書くと、上記のようになります。
私は、[∀k P(k) ⇒ ∀k P(k+1)] と勘違いしていました。
ある方が、次の極限値(nC[n/2] / (2^n))を求めたいようでした。
以下のように証明をしてみました。
[n] : ガウス記号
n!! : 2重階乗
===== ここから =====
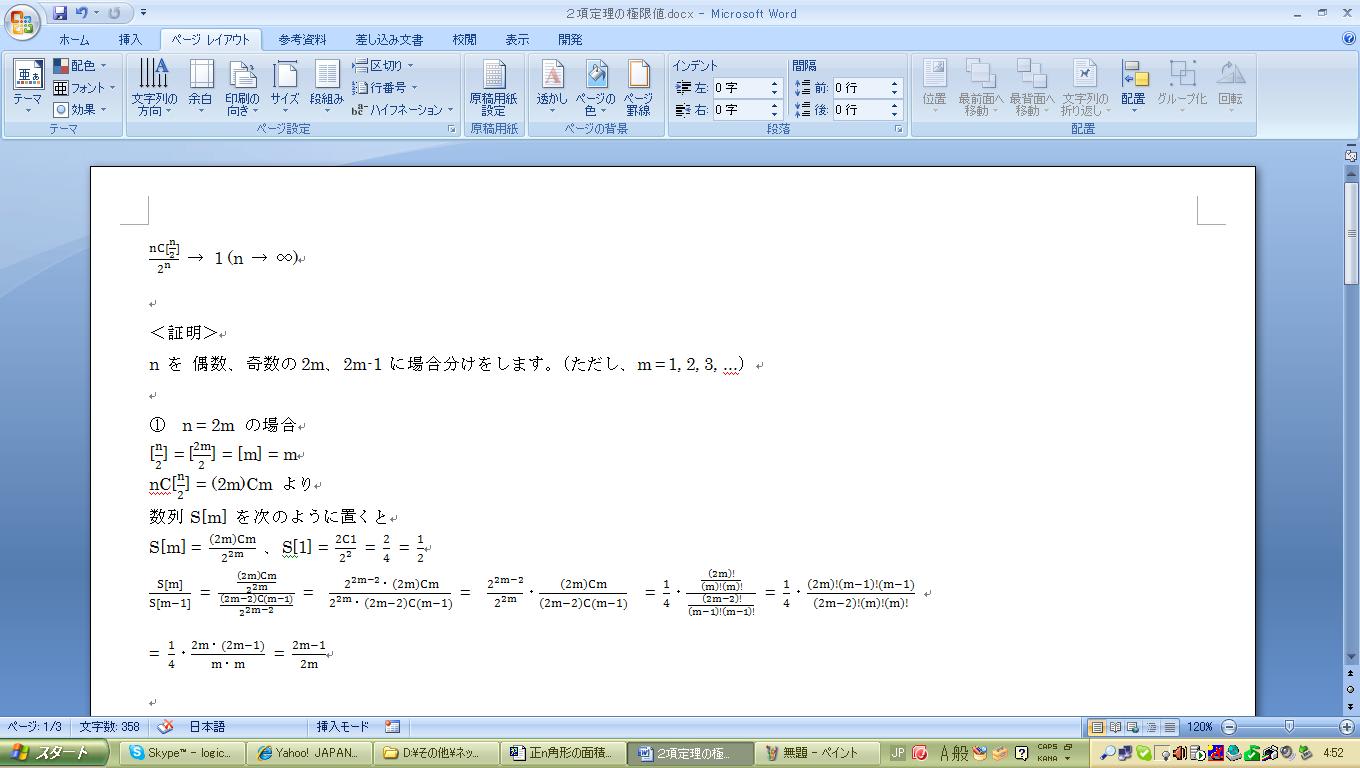
nC[n/2] / (2^n) → 1 (n → ∞)
極限値は「0」ではなく、「1」になります。
<証明>
n を 偶数、奇数の 2m、2m-1 に場合分けをします。(ただし、m = 1, 2, 3, ...)
① n = 2m の場合
[n/2] = [2m/2] = [m] = m
nC[n/2] = (2m)Cm より
数列 S[m] を次のように置くと
S[m] = (2m)Cm / {2^(2m)}
S[1] = 2C1 / (2^2) = 2 / 4 = 1 / 2
S[m] / S[m-1]
= [(2m)Cm / {2^(2m)}]/[(2m-2)C(m-1) / {2^(2m-2)}]
= {2^(2m-2)・(2m)Cm} / {2^(2m)・(2m-2)C(m-1)}
= {2^(2m-2)/2^(2m)}・{(2m)Cm / (2m-2)C/(m-1)}
= (1/4)・([(2m)!/{(m)!(m)!}] / [(2m-2)!/{(m-1)!(m-1)!}])
= (1/4)・([{(2m)!(m-1)!(m-1)!} / {(2m-2)!(m)!(m)!}])
= (1/4)・[{(2m)・(2m-1)} / {m・m}]
= (2m-1) / (2m)
②n = 2m-1 の場合
[n/2] = [(2m-1)/2] = [m - 1/2] = [(m-1) + 1/2] = m-1
nC[n/2] = (2m-1)C(m-1) より
数列 T[m] を次のように置くと
T[m] = (2m-1)C(m-1) / {2^(2m-1)}
T[1] = 1C1 / (2^1) = 1 / 2
T[m] / T[m-1]
= [(2m-1)C(m-1) / {2^(2m-1)}]/[(2m-3)C(m-2) / {2^(2m-3)}]
= {2^(2m-3)・(2m-1)C(m-1)} / {2^(2m-1)・(2m-3)C(m-2)}
= {2^(2m-3)/2^(2m-1)}・{(2m-1)C(m-1) / (2m-3)C/(m-2)}
= (1/4)・([(2m-1)!/{(m-1)!(m)!}] / [(2m-3)!/{(m-2)!(m-1)!}])
= (1/4)・([{(2m-1)!(m-2)!(m-1)!} / {(2m-3)!(m-1)!(m)!}])
= (1/4)・[{(2m-1)・(2m-2)} / {m・(m-1)}]
= (2m-1) / (2m)
①、②より
S[m] / S[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
S[1] = 1/2
T[m] / T[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
T[1] = 1/2
よって、偶数、奇数は
X[m] / X[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
X[1] = 1/2
より同じ数列になることが分かる。
X[m] = {(2m-1) / (2m)}・X[m-1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・X[m-2]
.....
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・X[2]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・X[1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・{1/2}
X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) ・・・(2)
nC[n/2] / (2^n) = X[m] より
nC[n/2] / (2^n) → 1 (n → ∞)
Q.E.D.
===== ここまで =====


(1) 証明の不備があれば、教えてください。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
どこからの本からの引用ではないので、極限値を確かめる方法がないため。
証明が合っているか、ないかを見て欲しいので、全内容を書きました。
※丸投げの意図ではなく、確認のためです。
※全内容は、自力で考えた内容です。
私の不安点は、(2)の部分です。
もし、この証明が合っていたならば、(1 + 1)^n = 2^n のとき、
(1 + 1)^n の最大値の nC[n/2] のとき、
nC[n/2] < (1 + 1)^n ⇔ nC[n/2] < 2^n なので、nC[n/2] / (2^n) < 1
でも、極限値は nC[n/2] / (2^n) → 1 (n → ∞) となる、不思議な結果になります。
===== 2012/01/11 AM9:25 追記 =====
数学のコミュに質問をしたら、丁寧に教えて頂きました。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
Wallis 積分から
(2m-1)!! / (2m)!! = (2/π) ∫_0^(π/2) (sin x)^(2m) dx → 0 (m → ∞)
X[m] → 0 (m → 0)より
nC[n/2] / (2^n) → 0 (n → ∞)
Wallis 積分は、とても勉強になりました。
以下のように証明をしてみました。
[n] : ガウス記号
n!! : 2重階乗
===== ここから =====
nC[n/2] / (2^n) → 1 (n → ∞)
極限値は「0」ではなく、「1」になります。
<証明>
n を 偶数、奇数の 2m、2m-1 に場合分けをします。(ただし、m = 1, 2, 3, ...)
① n = 2m の場合
[n/2] = [2m/2] = [m] = m
nC[n/2] = (2m)Cm より
数列 S[m] を次のように置くと
S[m] = (2m)Cm / {2^(2m)}
S[1] = 2C1 / (2^2) = 2 / 4 = 1 / 2
S[m] / S[m-1]
= [(2m)Cm / {2^(2m)}]/[(2m-2)C(m-1) / {2^(2m-2)}]
= {2^(2m-2)・(2m)Cm} / {2^(2m)・(2m-2)C(m-1)}
= {2^(2m-2)/2^(2m)}・{(2m)Cm / (2m-2)C/(m-1)}
= (1/4)・([(2m)!/{(m)!(m)!}] / [(2m-2)!/{(m-1)!(m-1)!}])
= (1/4)・([{(2m)!(m-1)!(m-1)!} / {(2m-2)!(m)!(m)!}])
= (1/4)・[{(2m)・(2m-1)} / {m・m}]
= (2m-1) / (2m)
②n = 2m-1 の場合
[n/2] = [(2m-1)/2] = [m - 1/2] = [(m-1) + 1/2] = m-1
nC[n/2] = (2m-1)C(m-1) より
数列 T[m] を次のように置くと
T[m] = (2m-1)C(m-1) / {2^(2m-1)}
T[1] = 1C1 / (2^1) = 1 / 2
T[m] / T[m-1]
= [(2m-1)C(m-1) / {2^(2m-1)}]/[(2m-3)C(m-2) / {2^(2m-3)}]
= {2^(2m-3)・(2m-1)C(m-1)} / {2^(2m-1)・(2m-3)C(m-2)}
= {2^(2m-3)/2^(2m-1)}・{(2m-1)C(m-1) / (2m-3)C/(m-2)}
= (1/4)・([(2m-1)!/{(m-1)!(m)!}] / [(2m-3)!/{(m-2)!(m-1)!}])
= (1/4)・([{(2m-1)!(m-2)!(m-1)!} / {(2m-3)!(m-1)!(m)!}])
= (1/4)・[{(2m-1)・(2m-2)} / {m・(m-1)}]
= (2m-1) / (2m)
①、②より
S[m] / S[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
S[1] = 1/2
T[m] / T[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
T[1] = 1/2
よって、偶数、奇数は
X[m] / X[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
X[1] = 1/2
より同じ数列になることが分かる。
X[m] = {(2m-1) / (2m)}・X[m-1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・X[m-2]
.....
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・X[2]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・X[1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・{1/2}
X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) ・・・(2)
nC[n/2] / (2^n) = X[m] より
nC[n/2] / (2^n) → 1 (n → ∞)
Q.E.D.
===== ここまで =====



(1) 証明の不備があれば、教えてください。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
どこからの本からの引用ではないので、極限値を確かめる方法がないため。
証明が合っているか、ないかを見て欲しいので、全内容を書きました。
※丸投げの意図ではなく、確認のためです。
※全内容は、自力で考えた内容です。
私の不安点は、(2)の部分です。
もし、この証明が合っていたならば、(1 + 1)^n = 2^n のとき、
(1 + 1)^n の最大値の nC[n/2] のとき、
nC[n/2] < (1 + 1)^n ⇔ nC[n/2] < 2^n なので、nC[n/2] / (2^n) < 1
でも、極限値は nC[n/2] / (2^n) → 1 (n → ∞) となる、不思議な結果になります。
===== 2012/01/11 AM9:25 追記 =====
数学のコミュに質問をしたら、丁寧に教えて頂きました。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
Wallis 積分から
(2m-1)!! / (2m)!! = (2/π) ∫_0^(π/2) (sin x)^(2m) dx → 0 (m → ∞)
X[m] → 0 (m → 0)より
nC[n/2] / (2^n) → 0 (n → ∞)
Wallis 積分は、とても勉強になりました。
平成23年5月23日に「かけ算には順序があるか」が発売がされました。
私は、特に専門の数学の分野はありません。
しかし、純粋数学を大学の数学科で学んだ者としては、「純粋数学の常識」と「一般の方の数学の常識」の違いに違和感を持ちました。
数学科は、数学を厳密に扱う分野ですけど、数学科以外の理工系(物理学、化学、生物学、工学など)だと、数学を道具として使う点は、数学科とは異なる印象を持っています。
<<著者の考え>>
著者は、かけ算の交換法則が常識であり、順序があるとは考えたことがなかった。
どうも、本の内容を読むと、数学の歴史、小・中・高の常識までの理解の範囲での記事の内容であった。
<<一般的な数学として>>
純粋数学では、解析学、代数学、幾何学を大きく分けると3つに分けることが出来ます。
ただし、最先端の純粋数学の研究では、明確には3つの分野は分かれていません。
<<代数学の群論より>>
代数学では、演算の公理を抽象的に定義して、さまざまな定理があります。
その代数学の中には、群論があります。
『群の公理』とは
群論とは、集合 G があります。
要素 x、y、z ∈ G があります。
① x × y ∈ G
② x × (y × z) = (x × y) × z (結合法則)
③ ∃e s.t. x × e = e × x = x for ∀x ∈ G (単位元の存在)
④ ∃a^(-1) s.t. a × a^(-1) = a^(-1) × a = e for ∀x ∈ G (逆元の存在)
この①、②、③、④を『群の公理』といいます。
※④を除くときの①、②、③をモノイド群(半群)と言います。
一般的に『群の公理』の演算子は「*」と表示します。
群論とは、集合 G があります。
要素 x、y、z ∈ G があります。
① x * y ∈ G
② x * (y * z) = (x * y) * z (結合法則)
③ ∃e s.t. x * e = e * x = x for ∀x ∈ G (単位元の存在)
④ ∃a^(-1) s.t. a * a^(-1) = a^(-1) * a = e for ∀x ∈ G (逆元の存在)
この①、②、③、④を『群の公理』といいます。
<注意>
「*」を「×」、「+」と入れかえてもよいです。
「×」のときを乗法群、「+」のときを加法群と区別をします。
『群の公理』の中では、x * y = y * x の交換法則はありません。
実は、次の(A)、(B)と区別します。
(A) x * y ≠ y * x (非可換群)
(B) x * y = y * x (可換群またはアーベル群)
代数学では、
(A) の非可換群は、一般的に純粋数学として考える事象です。
(B) の可換群(アーベル群)は、特別な事象として考えます。
小・中・高(数学Ⅱ・B)までは、(B) の可換群(アーベル群)について学んでいました。
一般的な非可換群で考えると、順序を区別します。
<<集合を考える>>
もう一度、『群の公理』を見て下さい。
集合 G とあります。
この集合 G とは、何を意味しているのでしょうか?
「かけ算には順序があるか」の集合 G は「自然数」を意味しているようです。
「自然数」は可換群(アーベル群)になります。
純粋数学では、集合 G は「実数」、「複素数」、「行列」、「四元数」などを意味しています。
「実数」、「複素数」は、可換群(アーベル群)になります。
「行列」、「四元数」は、非可換群になります。
<<数学者の考え(正確には代数学の考え)>>
「かけ算には順序があるか」の本の中には、数学者である、遠山教授や矢野教授の名前を出しています。
遠山教授の専門は、整数論、代数関数論です。
矢野教授の専門は、微分幾何学です。
遠山教授や矢野教授が、代数学として考えるとき、非可換群で考えることが一般的であることは知っています。
代数学より考えれば、非可環群なので順序を区別することは分かっていました。
しかし、厄介なことは、集合 G が、自然数や実数などのため、可換群になることです。
可換群なので、順序を必ず区別する必要はなかったのです。
集合 G が、可換群の自然数や実数などのため、「どちらでもいい」という、あいまいな表現となりました。
====「かけ算には順序があるか」の本(p14)より =====
数学教育協議会を率いて、日本の算数・数学教育に絶大な影響力を与えいた遠山啓の意見は、6×4 でも 4×6 でもどちらでもいい、というものです。
=========================================
それはなぜかというと、非可換群の身近な事柄がないため、一般の方に説明が出来なかったのです。
実際には、小・中・高(数学Ⅱ・B)までは、すべて可換群(アーベル群)についての計算を学ぶ内容になっています。
初めて、高校の「数学C」 の中で非可換群の行列を学ぶことになるのです。
<<まとめと結論>>
小学生には、1度は非可換群として「6×4」と「4×6」は順序を区別することを教えます。
それから、可換群(アベール群)なので、「6×4」と「4×6」の計算の結果の値は等しいので交換法則を教える。
という手順で教えることが算数・数学教育だと思います。
代数学では、非可換群が一般的であることを、前提に数学の議論をします。
その中で、可換群になる対象を研究します。
そういう意味では、可換群は特別な事象なのです。
大事なことは、非可換群を前提に意味を考えることが大事です。
「かけ算」、「たし算」の順序を区別する意味も含むことは分かると思います。
私は、特に専門の数学の分野はありません。
しかし、純粋数学を大学の数学科で学んだ者としては、「純粋数学の常識」と「一般の方の数学の常識」の違いに違和感を持ちました。
数学科は、数学を厳密に扱う分野ですけど、数学科以外の理工系(物理学、化学、生物学、工学など)だと、数学を道具として使う点は、数学科とは異なる印象を持っています。
<<著者の考え>>
著者は、かけ算の交換法則が常識であり、順序があるとは考えたことがなかった。
どうも、本の内容を読むと、数学の歴史、小・中・高の常識までの理解の範囲での記事の内容であった。
<<一般的な数学として>>
純粋数学では、解析学、代数学、幾何学を大きく分けると3つに分けることが出来ます。
ただし、最先端の純粋数学の研究では、明確には3つの分野は分かれていません。
<<代数学の群論より>>
代数学では、演算の公理を抽象的に定義して、さまざまな定理があります。
その代数学の中には、群論があります。
『群の公理』とは
群論とは、集合 G があります。
要素 x、y、z ∈ G があります。
① x × y ∈ G
② x × (y × z) = (x × y) × z (結合法則)
③ ∃e s.t. x × e = e × x = x for ∀x ∈ G (単位元の存在)
④ ∃a^(-1) s.t. a × a^(-1) = a^(-1) × a = e for ∀x ∈ G (逆元の存在)
この①、②、③、④を『群の公理』といいます。
※④を除くときの①、②、③をモノイド群(半群)と言います。
一般的に『群の公理』の演算子は「*」と表示します。
群論とは、集合 G があります。
要素 x、y、z ∈ G があります。
① x * y ∈ G
② x * (y * z) = (x * y) * z (結合法則)
③ ∃e s.t. x * e = e * x = x for ∀x ∈ G (単位元の存在)
④ ∃a^(-1) s.t. a * a^(-1) = a^(-1) * a = e for ∀x ∈ G (逆元の存在)
この①、②、③、④を『群の公理』といいます。
<注意>
「*」を「×」、「+」と入れかえてもよいです。
「×」のときを乗法群、「+」のときを加法群と区別をします。
『群の公理』の中では、x * y = y * x の交換法則はありません。
実は、次の(A)、(B)と区別します。
(A) x * y ≠ y * x (非可換群)
(B) x * y = y * x (可換群またはアーベル群)
代数学では、
(A) の非可換群は、一般的に純粋数学として考える事象です。
(B) の可換群(アーベル群)は、特別な事象として考えます。
小・中・高(数学Ⅱ・B)までは、(B) の可換群(アーベル群)について学んでいました。
一般的な非可換群で考えると、順序を区別します。
<<集合を考える>>
もう一度、『群の公理』を見て下さい。
集合 G とあります。
この集合 G とは、何を意味しているのでしょうか?
「かけ算には順序があるか」の集合 G は「自然数」を意味しているようです。
「自然数」は可換群(アーベル群)になります。
純粋数学では、集合 G は「実数」、「複素数」、「行列」、「四元数」などを意味しています。
「実数」、「複素数」は、可換群(アーベル群)になります。
「行列」、「四元数」は、非可換群になります。
<<数学者の考え(正確には代数学の考え)>>
「かけ算には順序があるか」の本の中には、数学者である、遠山教授や矢野教授の名前を出しています。
遠山教授の専門は、整数論、代数関数論です。
矢野教授の専門は、微分幾何学です。
遠山教授や矢野教授が、代数学として考えるとき、非可換群で考えることが一般的であることは知っています。
代数学より考えれば、非可環群なので順序を区別することは分かっていました。
しかし、厄介なことは、集合 G が、自然数や実数などのため、可換群になることです。
可換群なので、順序を必ず区別する必要はなかったのです。
集合 G が、可換群の自然数や実数などのため、「どちらでもいい」という、あいまいな表現となりました。
====「かけ算には順序があるか」の本(p14)より =====
数学教育協議会を率いて、日本の算数・数学教育に絶大な影響力を与えいた遠山啓の意見は、6×4 でも 4×6 でもどちらでもいい、というものです。
=========================================
それはなぜかというと、非可換群の身近な事柄がないため、一般の方に説明が出来なかったのです。
実際には、小・中・高(数学Ⅱ・B)までは、すべて可換群(アーベル群)についての計算を学ぶ内容になっています。
初めて、高校の「数学C」 の中で非可換群の行列を学ぶことになるのです。
<<まとめと結論>>
小学生には、1度は非可換群として「6×4」と「4×6」は順序を区別することを教えます。
それから、可換群(アベール群)なので、「6×4」と「4×6」の計算の結果の値は等しいので交換法則を教える。
という手順で教えることが算数・数学教育だと思います。
代数学では、非可換群が一般的であることを、前提に数学の議論をします。
その中で、可換群になる対象を研究します。
そういう意味では、可換群は特別な事象なのです。
大事なことは、非可換群を前提に意味を考えることが大事です。
「かけ算」、「たし算」の順序を区別する意味も含むことは分かると思います。










