
ブログを立ち上げたのが2007年3月で、半年毎に開設当初のことを振り返った記事を書いていましたが、3周年の今年3月にはうっかりしてこれを失念してしまいました。それもあって2007年頃の記事を読み返しています。また番号を打った連載記事なのに尻切れトンボになった記事もいくつかあり、これらはきちんと完結させたいと思っています。
その中で今回見直したいと思ったのは「滑り台の断面(その1)2007-07-13」と「滑り台の断面(その2)2007-07-14」です。
話は20年ほど昔に遡ります。滑り台は成型品を採用しなければ、鋼板またはSUS板をレーザーなどでカットしてから組み立てます。ローラー滑り台製造の立ち上がり頃、製作過程で滑り台の両側の板を溶接治具に入れて組み立てようとすると片方で鋼板が少し出っ張り、他方では少し足りないということがありました。特に中心線のRが小さくなるとこの傾向が強まりました。無理やり辻褄を合わせて溶接すると現場で強くテンションをかけて強制する事態に陥ります。
空間を通る傾き一定の3次元のクロソイドを中心線として、滑り台の幅を基準としてシフトさせた量、それに曲率と速度から決まる捻りを計算して両サイドの座標を計算して空間曲線を決定します。この曲線の従法線(接線と法線に垂直な線)を計算して板の形状を計算することは最初からの方針でした。計算のアルゴリズムは何度もチェックしたのですが、私の狙ったようなぴったりの仕上がりにはなりません。
ローラー滑り台の場合、滑走速度はせいぜい1.5m/s(≒6km/h)程度で、左右の傾きは7度程度です。グリッサンドの場合には最高速度が5m/sec(18km/h)以上になるので、速度と曲率から計算される捻りを省略することは安全上許されません。幅350mmの鋼板を切り出して以下のような断面で製作することは不可能だと悟りました。あとで分かったことですが、これが「ガウス曲率の工学的理解」でした。
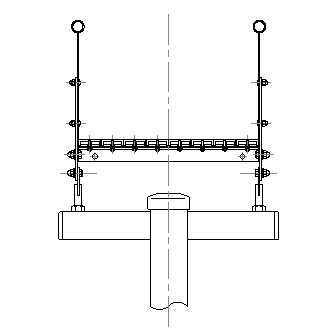
スピードが出ても、どのように曲がっても、計算上は滑走者のお尻が滑面のセンターに来るような断面でなければなりません。これを実現することは技術的に簡単なことではありませんでした。

工場の定盤の上で、例えばS字状の滑り台を組み立てて、現場で傾けて設置したとしましょう。鍛冶屋的には最も楽ちんな手法です。すると困った事にカーブではその傾斜分だけ外側に傾いてしまいます。運動する物体がこぼれ落ちる方向です。さらに困ったことには滑り台のセンターラインの接線と鉛直線の角度が一定ではなく、場所によって異なります。物体を落下させるmgsin(θ)のθ値が一定ではないというのはシミュレーションする時に演算を複雑にしてしまうことになります。これは避けたい。
沢山悪あがきして、到達したことは「曲面の内在的性質を知る必要がある」と言うことです。
↓ポチッと応援お願いします!

その中で今回見直したいと思ったのは「滑り台の断面(その1)2007-07-13」と「滑り台の断面(その2)2007-07-14」です。
話は20年ほど昔に遡ります。滑り台は成型品を採用しなければ、鋼板またはSUS板をレーザーなどでカットしてから組み立てます。ローラー滑り台製造の立ち上がり頃、製作過程で滑り台の両側の板を溶接治具に入れて組み立てようとすると片方で鋼板が少し出っ張り、他方では少し足りないということがありました。特に中心線のRが小さくなるとこの傾向が強まりました。無理やり辻褄を合わせて溶接すると現場で強くテンションをかけて強制する事態に陥ります。
空間を通る傾き一定の3次元のクロソイドを中心線として、滑り台の幅を基準としてシフトさせた量、それに曲率と速度から決まる捻りを計算して両サイドの座標を計算して空間曲線を決定します。この曲線の従法線(接線と法線に垂直な線)を計算して板の形状を計算することは最初からの方針でした。計算のアルゴリズムは何度もチェックしたのですが、私の狙ったようなぴったりの仕上がりにはなりません。
ローラー滑り台の場合、滑走速度はせいぜい1.5m/s(≒6km/h)程度で、左右の傾きは7度程度です。グリッサンドの場合には最高速度が5m/sec(18km/h)以上になるので、速度と曲率から計算される捻りを省略することは安全上許されません。幅350mmの鋼板を切り出して以下のような断面で製作することは不可能だと悟りました。あとで分かったことですが、これが「ガウス曲率の工学的理解」でした。

スピードが出ても、どのように曲がっても、計算上は滑走者のお尻が滑面のセンターに来るような断面でなければなりません。これを実現することは技術的に簡単なことではありませんでした。

工場の定盤の上で、例えばS字状の滑り台を組み立てて、現場で傾けて設置したとしましょう。鍛冶屋的には最も楽ちんな手法です。すると困った事にカーブではその傾斜分だけ外側に傾いてしまいます。運動する物体がこぼれ落ちる方向です。さらに困ったことには滑り台のセンターラインの接線と鉛直線の角度が一定ではなく、場所によって異なります。物体を落下させるmgsin(θ)のθ値が一定ではないというのはシミュレーションする時に演算を複雑にしてしまうことになります。これは避けたい。
沢山悪あがきして、到達したことは「曲面の内在的性質を知る必要がある」と言うことです。
↓ポチッと応援お願いします!

























