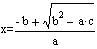受験生の皆さん

受験生の皆さん、数学の勉強はどうですか？

ネット電話でスキャナーがあれば、家庭教師は出来ますよ！
ご自分で、問題を用紙に書いて、スキャナーでPCに取り込んで、それをネット電話を通して、ファイル送信すれば、私がそれを印刷して、回答をしますよ！

私は、普通に教えることは出来ますけど、分からない方に教えることだけは苦手です。　すでに、出来ることが当たり前になっているので。

＜中・高の共通部分＞
・偏差値４０以下の方へ
教科書の公式を覚えて、基本的な問題を解きましょう！
何となくでも、いいのです。　教科書の公式を覚えることが近道です。

・偏差値４０～６０の方へ
教科書の公式が何となく覚えていたり、応用問題が出来る問題と出来ない問題がある感じでしょうか？
教科書の公式を復習します。　そして、少しだけの応用問題を解きます。
その応用問題は、解説が詳しい問題集であることがベストです。

・偏差値６０以上の方へ
自分の受験する高校・大学の過去の問を解く事をおすすめします。
どんな問題が出るのか？
不安があると思いますけど、学校で習った範囲しか出ません。
ただ、受験問題は、３、４つもひねった問題が多いのが事実です。

実は案外、公式を見落としている場合がありますので、公式を再確認することをおすすめします。
その上で、応用問題を解きましょう！

応用問題は、３種類ぐらいパターンがあります。
１．公式の応用問題。
２．各分野の融合問題。
３．数学的な独特な発想の問題

１．２．は公式と応用問題が解ければ自然と解けます。
３．だけは、本当の数学的なセンスが必要です。

質問などがありましたら、お気楽にコメントをください。

正弦定理と余弦定理

===== 数学A・Ⅰ =====
（三角形の基本性質）
A + B + C = 180°
|b - c| ＜ a ＜ b + c

（正弦定理）
a / sinA = b / sinB = c / sinC = 2R
※Rは△ABCの外接円の半径

a = 2RsinA、b = 2RsinB、c = 2RsinC
a : b : c = sinA : sinB : sinC

（余弦定理）
余弦定理は第１余弦定理と第２余弦定理の２つがあります。
受験では、第２余弦定理を頻繁に使用するので、余弦定理と言うと第２余弦定理を指します。

===== 第１余弦定理 =====
a = b・cosC + c・cosB
b = c・cosA + a・cosC
c = a・cosB + b・cosA

===== 第２余弦定理（余弦定理） =====
a² = b² + c² - 2・b・c・cosA
b² = c² + a² - 2・c・a・cosB
c² = a² + b² - 2・a・b・cosC

鈍角の三角比

===== 数学A・Ⅰ =====
x-y座標の半径rの円（半円）よりP(x, y)とすると
P₀(r, 0)とすると
∠P₀OP=θとすると（0°≦θ≦180°）

（定義）
sinθ = y / r
cosθ = x / r
tanθ = y / x (x ≠ 0)

（補角の公式）
sin(180°-θ) = sinθ
cos(180°-θ) = -cosθ
tan(180°-θ) = -tanθ

（補足）
sin(180°-θ) = -sin(θ-180°) = sinθ
cos(180°-θ) = cos(θ-180°) = -cosθ

（90°+θの公式）
sin(90°+θ) = cosθ
cos(90°+θ) = -sinθ
tan(90°+θ) = - 1 / tanθ

（補足）
sin(90°+θ) = sin(θ+90°) = cosθ
cos(90°+θ) = cos(θ+90°) = -sinθ

（三角比の相互関係）
tanθ = sinθ / cosθ
sin²θ + cos²θ = 1
1 + tan²θ = 1 / cos²θ
0°≦θ≦180°でも成り立ちます。

※三角関数よりθはどんな角でも成り立ちます。
※一般角の証明が必要なため、今の段階は0°≦θ≦180°で考えてよい。

直角三角形と三角比

===== 数学A・Ⅰ =====
△ABCより
∠C = 90°
BC = a、CA = b、AB = c とすると

（定義）
sinA = a / c
cosA = b / c
tanA = b / a

（三角比の相互関係）
tanθ = sinθ / cosθ
sin²θ + cos²θ = 1
1 + tan²θ = 1 / cos²θ

（余角の公式）
sin(90°-θ) = cosθ
cos(90°-θ) = sinθ
tan(90°-θ) = 1 / tanθ

===== 余角の公式の覚え方 =====
sin(-θ) = -sinθ、cos(-θ) = cosθ
90°づつ追加すると、sinθ ⇒ cosθ ⇒ -sinθ ⇒ -cosθ　以下は繰り返す⇒sinθ（元に戻る）
90°づつ減らすと、sinθ ⇒ -cosθ ⇒ -sinθ ⇒ cosθ　以下は繰り返す⇒sinθ（元に戻る）

ポイントは、θ-90°にすること（θが左になる）

sin(90°-θ) = -sin(θ-90°) = cosθ
sin(90°-θ) = -sin(θ-90°)は、sin(-θ) = -sinθより
-sin(θ-90°) = cosθは、90°づつ減らす、-sinθ⇒cosθより

cos(90°-θ) = cos(θ-90°) = sinθ
cos(90°-θ) = cos(θ-90°)は、cos(-θ) = cosθより
cos(θ-90°) = sinθは、90°づつ減らす、cosθ⇒sinθより

＜ポイント＞
１．sin(-θ) = -sinθ、cos(-θ) = cosθ
２．θ-90°にする
３．sinθ ⇔ cosθ ⇔ -sinθ ⇔ -cosθ
180°でも応用が利くので必ず覚えてください。

２次関数のグラフと２次不等式

===== 数学A・Ⅰ =====
（２次不等式の解）
ax² + bx + c = 0 のときの判別式D = b² - 4ac

a ＞ 0 の時
ax² + bx + c ＞ 0
D ＞ 0 のとき、x ＜ α、β ＜ x
D ＝ 0 のとき、x ≠ α
D ＜ 0 のとき、すべての実数

ax² + bx + c ＜ 0
D ＞ 0 のとき、α ＜ x ＜ β
D ＝ 0 のとき、解なし
D ＜ 0 のとき、解なし

ネット電話（無料）

最近、msnメッセンジャーを始めました。

・msnメッセンジャー
csnmath@hotmail.co.jp

・Skype
ID:logicalspace

２次関数のグラフと２次方程式

===== 数学A・Ⅰ =====
y = ax² + bx + c とx軸との共有点
D = b² - 4ac

D ＞ 0 ⇔ 異なる２点を共有する
D ＝ 0 ⇔ １点を共有する
D ＜ 0 ⇔ 共有点なし

２次関数のグラフ

===== 数学A・Ⅰ =====
（y = ax²)
a ＞ 0 のときは、下に凸
a ＜ 0 のときは、上に凸

（グラフの平行移動）
ここでは、一般関数についてです。
y = f(x)
x軸にp、y軸にqだけ平行移動すると
y - q = f(x - p) ⇒ y = f(x - p) + q

（グラフの特徴）
・y = a(x - p)² + q
軸は、x = p
頂点は、(p, q)
・y =ax² + bx + c
軸は、x = -b / 2a
頂点は、(-b / 2a, -(b² - 4ac) / 4a)

（最大、最小について）
y =ax² + bx + c を y = a(x - p)² + q に変形すると
・a ＞ 0 のとき、x = p で最小値（最大値はない）
・a ＜ 0 のとき、x = p で最大値（最小値はない）
※区間[t, s]の場合は、最大値、最小値は存在する

２次方程式

===== 数学A・Ⅰ =====
（２次方程式の解の公式）
ax² + bx + c = 0



ax² + 2bx + c = 0 (b ⇒ 2bの場合）



（２次方程式の実数解の個数）
ax² + bx + c = 0 の判別式 D とすると
D = b² - 4ac ＞ 0 ⇔ 異なる２つの実数解をもつ
D = b² - 4ac ＝ 0 ⇔ ただ１つの実数解（重解）をもつ
D = b² - 4ac ＜ 0 ⇔ 実数解を持たない。（異なる２つの複素数解をもつ）
※重解は正しい表現ではありません。　正しくは重根が正しいです。　大学の代数学入門で教えてもらうので、気にすることはありません。

（解と係数の関係）
ax² + bx + c = 0 の２つの解をα、βとすると
α + β = - b / a、α・β = c / a

（２次式の因数分解）
ax² + bx + c = 0 の２つの解をα、βとすると
ax² + bx + c = a(x - α)(x - β)
とくに、重解αをもつとき
ax² + bx + c = a(x - α)²


（補足）
３次方程式、４次方程式の解の公式は存在します。
５次方程式以上は、解の公式は存在しません。　数学者のガロアが公式がないことを証明しています。
ただし、５次方程式の解は、超越関数を使うと公式はあるようですが・・・。

もちろん、n次方程式の「判別式」と「解の係数と関係」もあります。
これは、代数学入門でならいます。

一次不等式

===== 数学A・Ⅰ =====
（不等式の性質）
１．a ＜ b ならば a + c ＜ b + c、a - c ＜ b + c
２．a ＜ b、0 ＜ c ならば ac ＜ bc、a / c ＜ b / c
３．a ＜ b、c ＜ 0 ならば ac ＞ bc、a / c ＞ b / c

平方根の計算

===== 数学A・Ⅰ =====
（平方数の平方根）
のとき
a ≧ 0 ならば a
a ＜ 0 ならば -a
つまり

（平方根の性質）
0 ＜ a、0 ＜ b とする
１．積と商


２．平方因数を根号の外へ出す。

３．分母の有理化



（二重根号をはずす）
0 ＜ a、0 ＜ b のとき
0 ＜ b ＜ a のとき

実数

===== 数学A・Ⅰ =====
（実数）
実数は、「有理数」と「無理数」に分かれます。
※無理数は、√2、1 - √5、πなど

有理数は、「整数」と「整数でない有理数」に分かれます。

整数は、「正の整数（自然数）」と「ゼロ」と「負の整数」に分かれます。
※正の整数（自然数）は、1、2、3、・・・
※ゼロは、0
※負の整数は、-1、-2、-3、・・・

整数ではない有理数は、「有限小数」と「循環小数」に分かれます。
※有限小数は、-2 / 5 = -0.4 など
※循環小数は、2 / 3 = 0.66666..... など

（絶対値の定義）
a ≧ 0 のとき |a| = a
a ＜ 0 のとき |a| = -a

因数分解

===== 数学I・A =====
<<< 因数分解の公式 >>>
ma + mb - mc = m(a + b - c)
a² + 2ab + b² = (a + b)²
a² - 2ab + b² = (a - b)²
a² - b² = (a + b)(a - b)
x² + (a + b)x + ab = (x + a)(x + b)
acx² + (ad + bc)x + bd = (ax + b)(cx + d)
a³ + b³ = (a + b)(a² - ab + b²)
a³ - b³ = (a - b)(a² + ab + b²)
a³ + 3a²b + 3ab² + b³ = (a + b)³
a³ - 3a²b + 3ab² - b³ = (a - b)³
a² + b² + c² + 2ab + 2ba + 2ca = (a + b + c)²
a³ + b³ + c³ - 3abc = (a + b + c)(a² + b² + c² - ab - ba - ca)

整式の加法・減法・乗法

===== 数学Ⅰ・A =====
<<< 基本法則 >>>
a + b = b + a
ab = ba
(a + b) + c = a + (b + c)
(ab)c = a(bc)
a(b + c) = ab + ac
(a + b)c = ac + bc

<<< 指数法則 >>>
m, nは整数のとき
a^maⁿ = a^{m + n}
(a^m)ⁿ = a^mn
(ab)^m = a^mb^m

<<< 乗法公式 >>>
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
(a + b)(a - b) = a² - b²
(x + a)(x + b) = x² + (a + b)x + ab
(ax + b)(cx + d) = acx² + (ad + bc)x + bd
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a - b)³ = a³ - 3a²b + 3ab² - b³
(a + b)(a² - ab + b²) = a³ + b³
(a - b)(a² + ab + b²) = a³ - b³
(a + b + c)² = a² + b² + c² + 2ab + 2ba + 2ca
(x + a)(x + b)(x + c) = x³ + (a + b + c)x² + (ab + bc + ca)x + abc

三平方の定理

===== 中３ =====
（三平方の定理）
a² + b² = c²