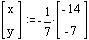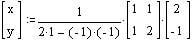===== 中1 =====
(比例)
y = 2x の場合
.....
(y, x) = (-4, -2)
(y, x) = (-2, -1)
(y, x) = (0, 0)
(y, x) = (2, 1)
(y, x) = (4, 2)
.....
y = ax の場合
.....
(y, x) = (-2a, -2)
(y, x) = (-a, -1)
(y, x) = (0, 0)
(y, x) = (a, 1)
(y, x) = (2a, 2)
.....
(反比例)
y = 2 / x
.....
(y, x) = (-1, -2)
(y, x) = (-2, -1)
(y, x) = (0, 0)
(y, x) = (1, 1)
(y, x) = (1, 2)
.....
y = a / x (x ≠ 0)
.....
(y, x) = (-a / 2, -2)
(y, x) = (-a, -1)
.....
(y, x) = (a, 1)
(y, x) = (a / 2, 2)
.....
<<< 一般形 >>>
比例:y = ax
反比例:y = a / x
<<< 抽象化 >>>
中学のレベルは、超える内容です。
なので、こんな風に考えるのだなあと感じて頂ければいいです。
x の値が決まれば、y の値が決まります。
これを、関数と言います。
f: x → y または y = f(x) と書きます。
この2つの書き方は、厳密には意味合いが少し異なる部分がありますが、現段階では、気にする必要はないと思います。
<<< 参考までに >>>
一応は、違いを書きますけど、現段階では覚える必要はありません。
f: x → y は、集合論での写像を表す書き方です。
y = f(x) は、解析学の関数を表す書き方です。
今回の比例、反比例は、関数の1部ととらえることが、普通なので、y = f(x) と書き表すことが一般的です。
厳密には、f: x → y の特殊な場合が、y = f(x)と考えます。
高校で習いますけど、x = 行列A, f = 行列M とすると y = MA = 行列B と表すことも出来ます。 この場合も、f: x → y とも表せます。