1.まえがき
あるサイトに、(0,∞)で定義された狭義の凸関数 f が lim [x→∞] f(x)=0 をみたすとき
(1) f(x)>0
(2) An=Σ[k=1,n] { f(k)-∫[k,k+1] f(x)dx } はn→∞で収束する。
(3) lim[n→∞]An > f(1)/2
を示せという問題があった。とても面白かったので以下に述べる。
2.証明
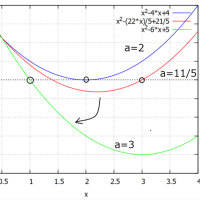
(1) 0<x<y<z<w とする。f は狭義の凸関数なので
(f(y)-f(x))(y-x)<(f(z)-f(y))/(z-y)<(f(w)-f(z))/(w-z)
となる。ここでw→∞とすると(f(w)-f(z))/(w-z)→0 となる。つまり
(f(y)-f(x))/(y-x)<(f(z)-f(y))/(z-y)≦0 だから
f(y)<f(x)・・・・(a)
つまり、f は狭義の単調減少関数である。このとき、もし f(x)≦0となる
x>0 があったとすると、(a)から f(y)<0 となるyがある。
つまり、y<zならば、f(z)<f(y)<0となり、z→∞でも f(z)→0
とならない。これは矛盾なので、x>0 ならば f(x)>0 となる。

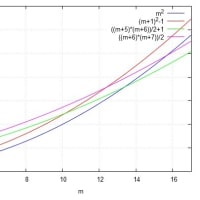
(2) (a)からf は(狭義の)単調減少なので k≦x≦k+1 ならば
f(k+1)≦f(x)≦f(k) だから、f(k+1)≦∫[k,k+1] f(x)dx≦f(k)
つまり、f(k)-∫[k,k+1] f(x)dx≧0 だからAnのΣ内の各項は0以上なのでAnは単調増加。さらに
An=Σ[k=1,n]{ f(k) - ∫[k,k+1] f(x)dx }≦Σ[k=1,n]{f(k)-f(k+1)}=f(1)-f(n+1)<f(1)
ゆえに、Anは単調増加で上に有界なので収束する。
(3) f は狭義の凸関数だから、区間(k,k+1)で
f(k)+{f(k+1)-f(k)}(x-k)>f(x)
が成立つことはあきらか。これを次の式に代入して
f(k) - ∫[k,k+1] f(x)dx>f(k)-∫[k,k+1]( f(k)+{f(k+1)-f(k)}(x-k) )dx
=f(k)-f(k)-{f(k+1)-f(k)}∫[0,1] x dx={f(k)-f(k+1)}/2
整理して次式をえる。
{f(k) - ∫[k,k+1] f(x)dx}>{f(k)-f(k+1)}/2・・・(b)

Σを取って
Bn=Σ[k=2,n]{f(k) - ∫[k,k+1] f(x)dx}>Σ[k=2,n]{f(k)-f(k+1)}/2=(f(2)-f(n+1))/2
ここで、n→∞とすれば、lim[n→∞]Bn ≧ f(2)/2になる。
この両式に(b)でk=1としたものを加えると
lim[n→∞]An=lim[n→∞]Bn+{f(1) - ∫[1,2] f(x)dx}> f(2)/2 + {f(1)-f(2)}/2=f(1)/2
となり結論を得る。極限をとると不等号「>」が「≧」になるところに工夫がいった。
補足
●はじめ、f(1)>0という条件があったが必要ないとわかった。
●上の議論で関数 f の連続性は積分のために必要と思ったが、関数 fは区間(a,b)で凸関数であれば、
区間(a,b)で連続になると教えていただいた。以下に概略
a<x<y<b とすると
(f(x)-f(a))/(x-a)≦(f(y)-f(x))/(y-x)≦(f(y)-f(b))/(y-b) となる。
M(x,y)=max{|f(x)-f(a)|/(x-a), |f(y)-f(b)|/(y-b)} とすれば
-M≦(f(y)-f(x))/(y-x)≦M となるから、|y-x|<δ=ε/M とすれば
|f(y)-f(x)|<ε を得る。x>y でも同じ議論ができる。
以上
あるサイトに、(0,∞)で定義された狭義の凸関数 f が lim [x→∞] f(x)=0 をみたすとき
(1) f(x)>0
(2) An=Σ[k=1,n] { f(k)-∫[k,k+1] f(x)dx } はn→∞で収束する。
(3) lim[n→∞]An > f(1)/2
を示せという問題があった。とても面白かったので以下に述べる。
2.証明
(1) 0<x<y<z<w とする。f は狭義の凸関数なので
(f(y)-f(x))(y-x)<(f(z)-f(y))/(z-y)<(f(w)-f(z))/(w-z)
となる。ここでw→∞とすると(f(w)-f(z))/(w-z)→0 となる。つまり
(f(y)-f(x))/(y-x)<(f(z)-f(y))/(z-y)≦0 だから
f(y)<f(x)・・・・(a)
つまり、f は狭義の単調減少関数である。このとき、もし f(x)≦0となる
x>0 があったとすると、(a)から f(y)<0 となるyがある。
つまり、y<zならば、f(z)<f(y)<0となり、z→∞でも f(z)→0
とならない。これは矛盾なので、x>0 ならば f(x)>0 となる。

(2) (a)からf は(狭義の)単調減少なので k≦x≦k+1 ならば
f(k+1)≦f(x)≦f(k) だから、f(k+1)≦∫[k,k+1] f(x)dx≦f(k)
つまり、f(k)-∫[k,k+1] f(x)dx≧0 だからAnのΣ内の各項は0以上なのでAnは単調増加。さらに
An=Σ[k=1,n]{ f(k) - ∫[k,k+1] f(x)dx }≦Σ[k=1,n]{f(k)-f(k+1)}=f(1)-f(n+1)<f(1)
ゆえに、Anは単調増加で上に有界なので収束する。
(3) f は狭義の凸関数だから、区間(k,k+1)で
f(k)+{f(k+1)-f(k)}(x-k)>f(x)
が成立つことはあきらか。これを次の式に代入して
f(k) - ∫[k,k+1] f(x)dx>f(k)-∫[k,k+1]( f(k)+{f(k+1)-f(k)}(x-k) )dx
=f(k)-f(k)-{f(k+1)-f(k)}∫[0,1] x dx={f(k)-f(k+1)}/2
整理して次式をえる。
{f(k) - ∫[k,k+1] f(x)dx}>{f(k)-f(k+1)}/2・・・(b)

Σを取って
Bn=Σ[k=2,n]{f(k) - ∫[k,k+1] f(x)dx}>Σ[k=2,n]{f(k)-f(k+1)}/2=(f(2)-f(n+1))/2
ここで、n→∞とすれば、lim[n→∞]Bn ≧ f(2)/2になる。
この両式に(b)でk=1としたものを加えると
lim[n→∞]An=lim[n→∞]Bn+{f(1) - ∫[1,2] f(x)dx}> f(2)/2 + {f(1)-f(2)}/2=f(1)/2
となり結論を得る。極限をとると不等号「>」が「≧」になるところに工夫がいった。
補足
●はじめ、f(1)>0という条件があったが必要ないとわかった。
●上の議論で関数 f の連続性は積分のために必要と思ったが、関数 fは区間(a,b)で凸関数であれば、
区間(a,b)で連続になると教えていただいた。以下に概略
a<x<y<b とすると
(f(x)-f(a))/(x-a)≦(f(y)-f(x))/(y-x)≦(f(y)-f(b))/(y-b) となる。
M(x,y)=max{|f(x)-f(a)|/(x-a), |f(y)-f(b)|/(y-b)} とすれば
-M≦(f(y)-f(x))/(y-x)≦M となるから、|y-x|<δ=ε/M とすれば
|f(y)-f(x)|<ε を得る。x>y でも同じ議論ができる。
以上