12歳以上 三段論法・対偶

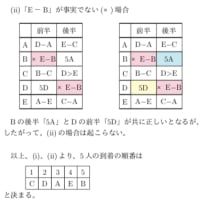
　次の条件が与えられているとき、論理的に正しいのはどれか。
・英語が得意な者は、12歳以上である。
・テニスが好きな者は、12歳以上である。
・12歳以上ならば数学が得意である。
１　12歳以上ならば、英語は得意である。
２　数学が得意ならば、英語も得意である。
３　12歳以上ならば、テニスが好きであり、かつ英語が得意である。
４　数学が得意でないならば、英語も得意でない。
５　12歳以下ならば、テニスが好きでない。





















【解説】
「英語が得意な者は、12歳以上である」を「英 → 12」、
「テニスが好きな者は、12歳以上である」を「テ → 12」、
「12歳以上ならば数学が得意である」を「12 → 数」と表す。

　　英 →12 → 数
　　テ →12 → 数　

三段論法より、
　　英 → 数
が成り立ち、その対偶は
　 ￢数 → ￢英
選択肢４「数学が得意でないならば、英語も得意でない」は正しい。

選択肢５について
　「テニスが好きな者は、12歳以上である」の対偶は「12歳未満ならばテニスがすきでない」となるので不適。

　　　　　　　　　　　　　　　　　正答　４