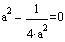面積の基本

面積の基本は、長方形だとご存じですか？

えっ！　本当・・・！？　という声が聞こえて来そうです。

長方形は、縦(a)×横(b) = ab が面積ですよね！
すべては、これが基本なんですよ！

平行四辺形も、変形すると長方形になりますね！
三角形は、その２つの三角形を組み合わせると、平行四辺形になりますね！


＜積分の考え方＞
y = x² を区間 [0, 1]の間の面積 S を求める方法は・・・？
区間[0, 1] を n分割します。
x0(= 0), x1, ... , x(N-1), xN(= 1)と分割します。

x(K-1), x(K) は、1/N となりますね！
y = x² は増加関数なので、x(K-1) ＜ x(K) ですね！

小さい面積 t(N)、大きい面積 T(N) を考えます。
t(N) は、x0, ... , X(N-1) を基準に考えます。
T(N) は、X1, ... , X(N) を基準に考えます。

x(K) の時の面積は、
x = x(K) は、x = K / N となるので、面積は x(K)²・(1 / N) = (K / N)²・(1 / N) となりますね！

t(N)
= x0²・(1 / N) + ... + x(N-1)²・(1 / N)
= (x0² + ... + x(N-1)²)・(1 / N)
= ((0 / N)² + ... + ((N-1) / N)²)・(1 / N)
= (0² + ... + (N-1)²)・(1 / N)³

T(N)
= x1²・(1 / N) + ... + x(N)²・(1 / N)
= (x1² + ... + x(N)²)・(1 / N)
= (x1² + ... + x(N)²)・(1 / N)
= (1² + ... + (N)²)・(1 / N)³


実際に求める面積を S とすると t(N) ＜ S ＜ T(N) となります。
N をどんどん大きな数にまで考えます。　最終的には∞まで考えます。
N → ∞ と書きます。

そうすると t(N) → S、T(N) → S となります。

1² + ... + n² = n(n + 1)(2n + 1) / 6 という公式があります。

t(N)
= (0² + ... + (N-1)²)・(1 / N)³
= (N - 1)N(2(N - 1) + 1) / 6・(1 / N)³
= (N - 1)N(2N - 1) / 6・(1 / N)³
= (1 - 1 / N)・1・(2 - 1 / N) / 6

N → ∞ とすると 1 / N → 0 となるので
t(N) → (1 - 0)・1・(2 - 0) / 6 = 2 / 6 = 1 / 3

T(N)
= (1² + ... + (N)²)・(1 / N)³
= N(N + 1)(2N + 1) / 6・(1 / N)³
= 1・(1 + 1 / N)(2 + 1 / N)

N → ∞ とすると 1 / N → 0 となるので
T(N) → 1・(1 + 0)(2 + 0) / 6 = 2 / 6 = 1 / 3

よって、
t(N) ＜ S ＜ T(N) を N → ∞ とすると
t(N) → 1 / 3、T(N) → 1 / 3 なので、
1 / 3 ＜ S ＜ 1 / 3 なので S = 1 / 3 となります。
※これを「はさみうちの原理」と言います。

求める面積は、S = 1 / 3


面積は長方形が基本なのは、分かって頂けましたでしょうか？

代数多様体

代数多様体の双有理分類をめざして
代数多様体について

代数多様体というと、広中平祐教授が「代数多様体における特異点の解消」よりフィールズ賞を受賞したことが懐かしいです。

オイラーの見た夢

メインの話題は、ゼータ関数です。

＜ゼータ関数＞
ζ(s)
= ∑n^-s
= 1 + 2^-s + 3^-s + ...
= 1 + 1/2^s + 1/3^s + ...

ζ(-1) = 1 + 2 + 3 + ... = -1/12
複素数まで考えて、解析接続をすれば、ζ(-1) = -1/12 となるようです。
※解析接続の意味はよく知りません。
※解析接続についてを読みましたが、なんとなくしか分かりません。

現在、知られている最大の素数は、2008年8月23日に発見されています。
メヌセンス素数（2ⁿ - 1 の形）
2^43112609 - 1 （1297万8189桁）

ζ(-1)
= 1 + 2 + 3 + ... = -1/12
ζ(-2)
= 1 + 2² + 3² + ... = 0
ζ(-3)
= 1 + 2³ + 3³ + ... = 1/120
ζ(-4)
= 1 + 2⁴ + 3⁴ + ... = 0
※ s の負の偶数は、ζ(s) = 0 になることは知られている。

数学者リーマンは、ゼータ関数である予想をしました。
リーマン予想：ζ(s) の虚の零点の実部はすべて 1/2 であろう。

ヒルベルトの２３の問題の１つにリーマン予想（第８問題）があります。
ところで、ヒルベルト２３の問題は、現在はどれだけ解かれているのでしょうか？
私は、簡単な解説書を持っているので、２３の問題は知っていますが、どれだけ解かれているのでしょうか？

※ご指摘があったので、１部内容を修正しています。

数学者の夢

オイラーの見た夢／無限和の夢
代数多様体の双有理分類をめざして
微分幾何と他分野との狭間で見えるもの
７次方程式の解法を夢見た数学者フェリックス・クライン
可積分系だって現在数学である
万物の幾何学へかける夢
ゲーテルの夢
終わりなき旅
人や社会を数理モデルで研究すること
カルタンの夢
が数学セミナーの記事のタイトルです。

数学セミナーを読みました。
現在は、「７次方程式の解法を夢見た数学者フェリックス・クライン」を途中まで読んでいるところです。

「数学の最先端　２１世紀への挑戦」が１～６巻まで発売されているようですね！
こんな本があると欲しくなります。

改めて見ると、このような記事を読むとワクワクする感じです。
数学は楽しいなぁ・・・。

円周率

円周率π = 3.14159265358979.....
までは、記憶しています。

小５で習いますね！
円周率 = 3.14 と教わりました。

中学から、円周率をπと表現するようになります。

πの定義は、直径１の円周の長さとしました。
※半径１の面積が定義ではありません。

近似値を求める方法は、円に「内接する n角形」と「外接する n角形」辺の長さを求める方法です。
円に「内接する n角形」をL₁
円に「外接する n角形」をL₂
とすると
L₁ ＜ π ＜ L₂ となります。

5角形で考えてみると、5sin36° ＜ π ＜ 5tan36°
sin36° = 0.5878
tan36° = 0.7265
よって、　2.9390 ＜ π ＜ 3.6325

同様にn角形では、n・sin(180°/ n) ＜ π ＜ n・tan(180° / n)

では、20角形を考えてみましょう！
20・sin9° ＜ π ＜ 20・tan9°
20・0.1564 ＜ π ＜ 20・0.1584
3.128 ＜ π ＜ 3.168

正確にπを求める方法はないのでしょうか？
それは、マチンの級数が有名です。
π = 16arctan(1 / 5) + 4arctan(1 / 239)

他に求め方は、色々と発見されています。
プログラムでは、このマチンの級数を使って求めることが出来ます。

πは無理数であることが分かりました。
無理数でも、特別な無理数で超越数があります。
√2 は無理数です。　しかし、x² = 2 の解ですね！
n次方程式の解にならない無理数を、超越数と言います。
πは超越数であることが分かりました。

複雑系について

nanaponさんより「複雑系」を取り上げていました。

===== nanaponさんのコメント =====
>本当に複雑系について知りたいのかな？
と言われると困りますが、猿でもわかるくらいには興味あります。

と言うことで、複雑系のイメージについて書きたいと思います。

＜学問から社会へ＞
数学の研究⇒物理学の応用⇒社会での活用　という順番で学問から社会への応用となります。

例えで言えば、携帯電話を想像して見てください。
通信でやり取りをしているのは、電波ではないでしょうか？

数学の研究では、三角形より三角関数を研究しました。　※高校で習う、sin、cos、tanですね！
物理学の応用では、波（電波など）を応用して研究しました。
社会では、携帯のやり取りに電波を利用しました。

数学の研究（三角関数）⇒物理学の応用（波）⇒社会（携帯電話の電波）

数学の研究⇒物理学の応用⇒社会での活用という流れを頭に置いて欲しいと思います。


＜複雑系＞
複雑系の場合は、数学の研究⇒社会での活用となり物理の応用がありません。
※もちろん、物理で研究している方はいます。

数学の研究（カオス・フラクタル）
社会では、複雑な経済（複雑系経済学）

という風に複雑系を扱います。

私が言っているのでは、数学の研究のカオス・フラクタルのことです。
nanaponさんが言っているのが、社会での複雑系経済学のことだと思います。

つまり、私は複雑系の出発点を言っています。　nanaponさんは、複雑系の応用についての記事を書かれているのですね！


＜カオスとフラクタル＞
＜画像の数式＞
カオスとフラクタルの図形より

カオスの例です。
離散系のカオス（１）の「2．翼のようなストレンジアトラクタ」を見て下さい。

３つの画像がありますね！
x_{n + 1} = ax_n + by_n + c + d/(1+x_n²) ・・・①
y_{n + 1} = -x_n　・・・②

３つの画像は、①、②の数列を描いた物なのです。　※数列は高校で習います。

左の画像：a=-0.9，b=0.96，c=-4.0，d=5.0, x0=1.0，y0=0.0
中の画像：a=-1.57，b=0.96，c=-4.0，d=5.0, x0=1.0，y0=0.0
右の画像：a=-1.76，b=0.96，c=-4.0，d=5.0, x0=1.0，y0=0.0

３つの画像は、aの値が異なるだけで、他は同じです。
しかし、画像として見ると、全く違う数列の画像に見えます。

同じことを書きますが、カオスとは、初期値によって、結果が変わることです。
つまり、aの値によって、画像が違うので、これがカオスであります。
※aの値が初期値、画像が結果です。


フラクタルの例です。
マンデルブロ集合の「1．f(z)=z²+c」を見てください。

４つの図がありますね！
f(z)=z²+c・・・③

４つの画像は、③の複素数列を描いた物なのです。　※複素数列は理系の大学２年生で習います。

左から順番に、X1、X2、X3、X4と名前を付けます。
X1：z0=0, c=a+bi, a：-1.485～-1.473, b：-0.006～0.006
X2：z0=0, c=a+bi, a：-1.266～-1.246, b：0.371～0.391
X3：z0=x0+y0i, c=-0.035+0.795i, x0：-1.4～1.4，y0：-1.4～1.4
X4：z0=x0+y0i, c=-0.704+0.28i, x0：-0.27～0.13，y0：0.51～0.91

４つの画像は、同じ複素配列を見ていますが、見る範囲によって見え方が異なるということです。

同じことを書きますが、フラクタルとは、図形の配置（繰り返し処理を含む）です。
※図形の配置が複素数列となります。

※繰り返し処理の事を、数学の用語では自己相似性と言います。
===== 数学的な自己相似形について =====
③の式は、z_{n + 1} = z_n + cが正確な表現です。
f_{n + 1}(z) = f_n(z) と f を n 回繰り返していますね！
この f を n 回繰り返していることが、自己相似性と言います。
もちろん、n → ∞ とすれば、限りなく表現できることは分かると思います。
===== ここまで =====

ただし、フラクタルは、次のことが必要十分条件です。 つまり、フラクタルの定義です。

＜フラクタルの定義＞
集合Ｋの位相次元　dim_Ｔ(Ｋ) とハウスドルフ次元　dim_Ｈ(Ｋ)について、
dim_Ｔ(Ｋ) ＜ dim_Ｈ(Ｋ)
が成立するとき、集合Ｋはフラクタルであるという。
※位相、ハウスドルフ、次元とかは、数学用語なので、理系の方を除いて理解する必要がありません。
数学的には、フラクタルの定義は必要でありますが、複雑系を考える時には、フラクタルの定義に重きを置く必要はありません。


＜複雑系経済学＞
カオスとフラクタルからは、何を学んだのでしょうか？
・初期状態によって、結果が異なる（カオス）
・同じ物でも範囲が異なれば見方が異なる（フラクタル）

複雑系経済学では、一般に非線形で、要素間の相互依存性が強い系は複雑系となる可能性がある。
特に経済学にとっては要素の数が多いことや収穫逓増現象が重要である。

要素間の相互依存性が強い系とは、複数の初期状態と異なる結果には、因果関係があるということですね！
この相互依存性を因果関係と言っているので、何だか難しいように聞こえますね！

私は、複雑系経済学は専門外なので、簡単にしか触れません。


nanaponさんの「田坂広志さんのメルマガから引用」して「複雑系」を取り上げています。
田坂広志さんは、経済を複雑系経済学の１側面として考えて取り上げていると思います。


===== LogicalInSpaceの感想 =====
単純化と複雑系のどちらが良いのか？　議論を呼ぶと思いますけど。　研究する範囲では、両方が必要であると思います。
社会では、どのようにアプローチするのかが重要なことであると思います。
世の中（自然界、経済）は、簡単な事より複雑な事の方が多い事も事実だと思います。
複雑系経済学は、まだまだ進化する学問だと思いますし、実経済もどんどん変化すると思います。

前回の記事をもう１度、読んでみてください。　少しイメージが出来ると思いますよ！

数学の本を読みました

代数幾何学、実関数とfourie（フーリエ）解析１・２を読みました。

「代数・幾何（高校）」と「代数幾何（大学以上）」とは違います。
「・」が付くだけで全然内容は異なります。

・代数・幾何（高校）
（ベクトル・空間図形・行列・１次変換・２次曲線）


読んだ本は以下です。
・代数幾何入門
（射影空間と射影多様体・代数曲線・代数曲線の解析的理論）
・実関数とFourie解析１・２
（Fourie級数・Fourie級数と応用・実関数の性質（Ⅰ・Ⅱ）・Fourie変換・Fourie変換と応用・関連する話題）


岩波書店の「現代数学への入門」、「現代数学の基礎」、「現代数学の展開」があります。
私は、「現代数学の基礎」の１部を持っています。
「実関数とFourie解析１・２」は「現代数学の基礎」の１つの本です。

ちょっとしたこと

i：虚数単位

x² = -1 の解が x = ±i

ところで、x² = i の解は存在するのでしょうか？
このちょっとしたことを考えてみたいと思います。

x = a + biとすると
x² = (a + bi)² = a² - b² + 2abi = i より

a² - b² = 0
2ab = 1






a は実数より a² > 0 なので





が解となります。

なので、複素数まで数を拡張すれば、それ以上は拡張する必要はないようです。

数について

===== 小学 =====
自然数 Z：1、2、3、4、5、6...
小数：0.3、0.5、0.134...
分数：1/2、4/9... (有理数 Q：a / b)
※自然数、有理数は、中学で習う言葉
※自然数 Z、有理数 Qは、アルファベットの表記は高校で習う

===== 中学 =====
整数 N：...-3、-2、-1、0、1、2、3...
実数 R：√2、π...
※整数 N、実数 Rは、アルファベットの表記は高校で習う

===== 高校 =====
複素数 C：2 + i、√5 - 3i... (a + bi: 実数R：a、b)
※i は虚数単位

フェルマーの最終定理

===== 数学一般 =====
フェルマーの最終定理、フェルマーの大定理とか呼ばれています。
（整数N:x、y、z、n）
xⁿ + yⁿ = zⁿ
n ≧ 3 の時、x、y、zを満たす整数解は、存在しない。