それはこれだ・・・・！
しばらく考えた！！
何とか解けた・・・！？
面白いから、考えて・・・・。
敢えて、今回は書かないでおこう。勿論、数学の問題だが、理論的に解く必要がある。
分かった人は、コメントへどうぞ！
最新の画像［もっと見る］
-
ロバートF.ケネディジュニア警告！如何なる場合もCOVID-19ワクチンを拒否！
4年前
-
ロバートF.ケネディジュニア警告！如何なる場合もCOVID-19ワクチンを拒否！
4年前
-
ロバートF.ケネディジュニア警告！如何なる場合もCOVID-19ワクチンを拒否！
4年前
-
ロバートF.ケネディジュニア警告！如何なる場合もCOVID-19ワクチンを拒否！
4年前
-
ヒラリークリントンの逮捕から絞首刑までーその４ー
4年前
-
ヒラリークリントンの逮捕から絞首刑までーその４ー
4年前
-
ヒラリークリントンの逮捕から絞首刑までーその４ー
4年前
-
ヒラリークリントンの逮捕から絞首刑までーその４ー
4年前
-
ヒラリークリントンの逮捕から絞首刑までーその３ー
4年前
-
ヒラリークリントンの逮捕から絞首刑までーその３ー
4年前
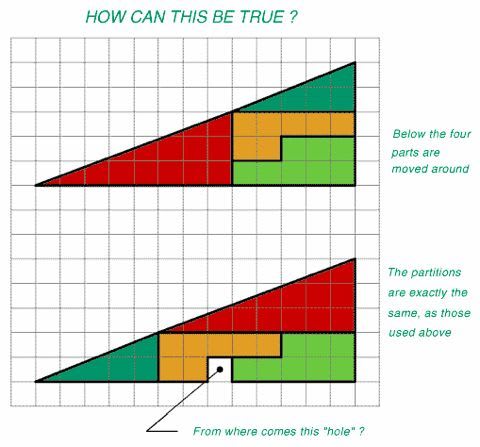
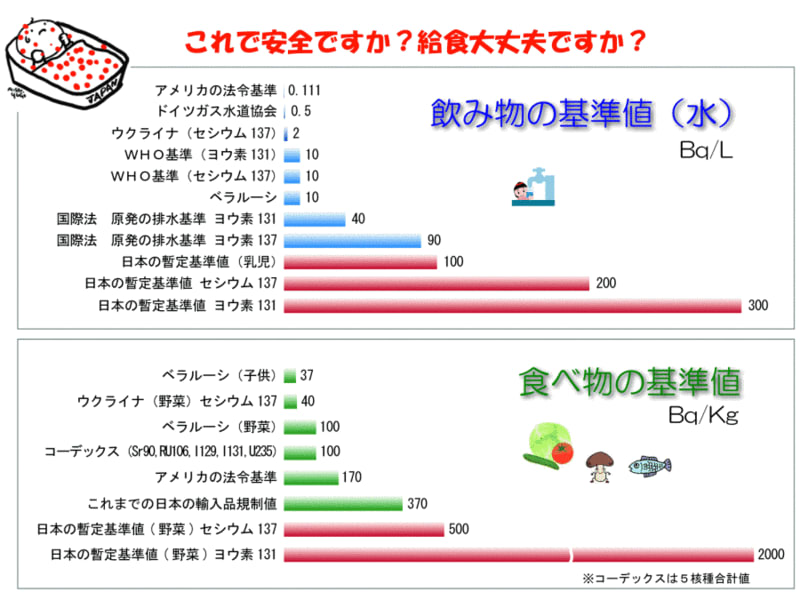
ちょっと線がずれてんじゃないの？
うん、ちょっとずれてるけど
ちょっとずれたらだめなのよ
祖母は奈良女子大出の数学の先生でした。
で、みなさん回答しているようなことですが、「ちょっとずれてる」ことを直観で分かるように言いますと、上の三角形の斜辺は下にへこんでいます。下の三角形の斜辺は上に出っ張っています。二つ重ねるとずれた部分が薄い菱形になります。その菱形の面積が穴ぼこの面積ですね、きっと。
ななめの辺が微妙に直線ではありません。
分からないように、都合の良いように、引かれています。
皆さん、すでに正解が出ているようですね。
大きな長方形13x5=65
色図形の面積の和=(5+7+8+12)x2=64
(長方形の面積)-(色図形)=65-64=1
＜返事＞
すもも 様
コメント有り難うございます。
面白い解ですね。論証と言うよりも、実証と言うべきですね。
有り難うございました。
飄平
要は、上下の二つ共に「三角形ではない」という事に気付けば、後は早いんですよね。
小さな三角形のどちらも「大きな三角形（に見えるもの）」と相似ではない以上、上下二つ共の図形の斜めのラインは「直線」ではないから。
上下の組み合わせとも、黄色のパーツの直角部分を境に三角形の斜めのラインが繋がってる、というのが錯覚を起こし易いポイントでしょうね。考えた人は偉いw
＜返事＞
つむじ曲がり 様
コメント有り難うございます。
その通りですね。いやあ～、あんまり簡単だったみたいですね。当ブログの読者諸氏は、真相を見究めるお目が高い。
これは誇りです。有り難うございました。後で、論証し解きます。
飄平
赤の三角は底辺が８の高さが３の勾配が３／８です。
エメラルドグリーンの三角底辺が５の高さが２の勾配がは２／５です。
勾配の目の錯覚によるトリックだと思います。
面積的には、赤（１２）エメ（５）黄（７）緑（８）の３２だと思います。
上の図の赤の上の台形の面積は（２＋５）×8/２の２８
エメの上は２×５／２の５で足して３３で１３×５の６５から引いて３２です。
下の図はエメの上の台形の面積は（３＋５）×５/２の２０
赤の上は３×８/２の１２で足して３２で６５から引いて３３です。
その差１がトリックの１だと思います。
8
＜返事＞
8 様
コメント有り難うございます。
その通りです。私の論証に近い。三角関数で解くと判りやすいですね。有り難うございました。
飄平
回答ですが、一見直角三角形に見える斜辺は直線では有りません。
上手では斜辺が若干凹んでいますが、下図の斜辺はマス一目の面積分
凸っているという事ですね。
晩酌中なので間違っているかも・・・！？
＜返事＞
８８８（スリーエイト） 様
コメント有り難うございます。
いつも阿修羅に転載頂き、有り難うございます。
仰るとおりです。でも、又、しらふの時、論証して頂ければ、面白い説明があり得ると思います。
本当にご苦労様。協賛有り難うございました。
飄平
アルコールが入ってるので間違ってるかもしれません
赤の三角の鋭角と緑の方の三角の鋭角が違ってるので
上の図は全体で三角形になってないと思いますが
それとも他のトリックか？
＜返事＞
すぎもとたかふみ 様
コメント有り難うございます。
その通りです。しらふの時でも、論証して下されば、有り難い。
ご協賛有り難うございます。
飄平
いつもタメになるブログをありがとうございます。
さて、今回の問題の回答です。
＜以下、回答＞
この絵が正しいのは「上に並べた形が、実は三角形ではない」からです。
仮に一マスを1cmとすると、4つの図形の面積の合計は32?です。
・赤の三角形 3×8÷2=12
・緑の三角形 2×5÷2=5
・黄色の図形 7
・黄緑の図形 8
ここで、赤の三角形と緑の三角形の底辺:高さの辺の比を考えると、赤が8:3に対して緑は5:2となり、相似ではありません。
そのため、並べ方によって下の図のようにスキマができてしまうのです。
そして、なぜスキマが1マス分だけ余るのかについては、三角形ではなく13×5=65?の長方形で考えます。
4つの図形を2倍すると合計で64?となり、65-64=1?がどこかに余ってしまうのです。
・赤の三角形 12×2=24
・緑の三角形 5×2=10
・黄色の図形 7×2=14
・黄緑の図形 8×2=16
その余りを、下の図ではあの場所に持っていったわけです。
＜以上＞
いかがでしょうか？
答えはおそらく合っていると思うのですが、きちんと説明できたかどうかは不安です。
これからも頑張ってください。応援しております。
＜返事＞
Specialweek 様
コメント有り難うございます。
ご丁寧なご説明、痛み入ります。
その通りだと思います。説明の仕方はそれぞれですが、同じです。
少し、説明の仕方は違いますが・・・・。私の説明は本稿で！
協賛して頂いて、有り難うございます。
飄平