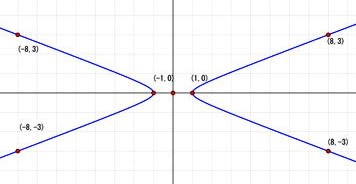
先日の記事で2次の無理数の連分数展開とペル方程式の関係について書きました。両者が深くつながっていることに興味を持ち、簡単ではありますがペル方程式の解法について書いてみる気になりました。

の最小解の組が(8、3)であることは分かっているとして話を進めます。つまり
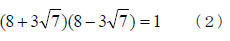
を満たします。
さてx=8+3√7を解とする全ての係数が整数の2次方程式を作るのは簡単で、8を移項して平方するだけです。

2次方程式なので解は二つあって、もう一つはx=8-3√7です。
この解を改めて

と書きます。√7は整数の四則演算からは得られない数であることに注意しましょう。
二つの解は互いに共役であると考えられ、複素数と同じような扱いが可能です。整数の集合Zに無理数√7を添加した集合を考え、その任意の要素をα、βとします。すると以下のような関係が成り立ちます。

共役の考えが分かったところでペル方程式の解の集合について考えて見ましょう。いま、整数x、yがこの方程式の解だとします。つまり
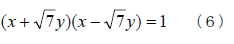
を満たします。

とすれば

は明らかです。ここで解集合をKとし、その任意の要素をα、βとします。
そしてα∈K、β∈Kならばαβ∈Kがいえます。なぜなら

と言う関係から
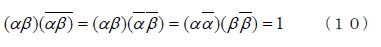
が言えます。つまり解集合の任意の二つの解αとβを選んで掛け合わせると、それもまた解であることが分かります。早い話が、Kは乗法に関して可換群となっているのです。
またαβ∈Kから、β=αとすれば
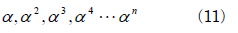
は全てこの方程式の解であることも分かります。
ここでフリーの数式処理ソフトwxMaximaを使って6乗までの計算をさせてみました。

解の組は(127,48),(2024,765),(32257,12192),(514088,194307),(8193151,3096720)と次々に求まります。どうやら全ての解はαのべき乗で表せそうですが、これ以外の解は存在するでしょうか?存在しないことが以下のように背理法で証明することが出来ます。ここで取り扱っているのは冒頭のグラフの第一象限だけを考えているので1<αで、αが解の最小値です。従って
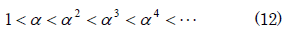
が成り立ちます。もしαのべき乗で表されていない解βが存在し、或る自然数nで

となり、αがKの最小値であることに矛盾する。従って全ての解は最小値αのべき乗で表現されることが証明されました。
ここでペル方程式の一般的解法に辿り着きました。Nを平方数ではない正の整数とする方程式

のyに自然数を次々に代入して、xが整数となる最小解を見つける。これをαとすれば全ての解を求めることが出来ます。最初に戻って(1)の最小解は
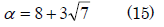
でしたから、その共役数
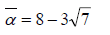
を使って一般解を以下のように書くことが出来ます。

この作業を通じて、少しですが代数感覚が戻ったようです。でも先は長い。
参考文献を掲げておきます。これは最低限の礼儀です。
1、ゲリファント他著『方程式の解き方』東京図書1993年
2、北村泰一著『数論入門』槇書店1986年
3、石谷茂著『現代数学と大学入試 Ⅱ』現代数学社1972年
Mathematicaの出力結果だけをいきなりコメントするなんてサイテーです。
↓ポチッと応援お願いします!


の最小解の組が(8、3)であることは分かっているとして話を進めます。つまり
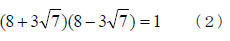
を満たします。
さてx=8+3√7を解とする全ての係数が整数の2次方程式を作るのは簡単で、8を移項して平方するだけです。

2次方程式なので解は二つあって、もう一つはx=8-3√7です。
この解を改めて

と書きます。√7は整数の四則演算からは得られない数であることに注意しましょう。
二つの解は互いに共役であると考えられ、複素数と同じような扱いが可能です。整数の集合Zに無理数√7を添加した集合を考え、その任意の要素をα、βとします。すると以下のような関係が成り立ちます。

共役の考えが分かったところでペル方程式の解の集合について考えて見ましょう。いま、整数x、yがこの方程式の解だとします。つまり
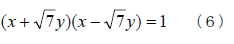
を満たします。

とすれば

は明らかです。ここで解集合をKとし、その任意の要素をα、βとします。
そしてα∈K、β∈Kならばαβ∈Kがいえます。なぜなら

と言う関係から
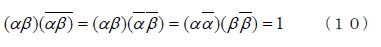
が言えます。つまり解集合の任意の二つの解αとβを選んで掛け合わせると、それもまた解であることが分かります。早い話が、Kは乗法に関して可換群となっているのです。
またαβ∈Kから、β=αとすれば
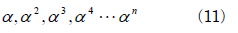
は全てこの方程式の解であることも分かります。
ここでフリーの数式処理ソフトwxMaximaを使って6乗までの計算をさせてみました。

解の組は(127,48),(2024,765),(32257,12192),(514088,194307),(8193151,3096720)と次々に求まります。どうやら全ての解はαのべき乗で表せそうですが、これ以外の解は存在するでしょうか?存在しないことが以下のように背理法で証明することが出来ます。ここで取り扱っているのは冒頭のグラフの第一象限だけを考えているので1<αで、αが解の最小値です。従って
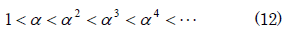
が成り立ちます。もしαのべき乗で表されていない解βが存在し、或る自然数nで

となり、αがKの最小値であることに矛盾する。従って全ての解は最小値αのべき乗で表現されることが証明されました。
ここでペル方程式の一般的解法に辿り着きました。Nを平方数ではない正の整数とする方程式

のyに自然数を次々に代入して、xが整数となる最小解を見つける。これをαとすれば全ての解を求めることが出来ます。最初に戻って(1)の最小解は
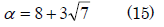
でしたから、その共役数
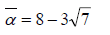
を使って一般解を以下のように書くことが出来ます。

この作業を通じて、少しですが代数感覚が戻ったようです。でも先は長い。
参考文献を掲げておきます。これは最低限の礼儀です。
1、ゲリファント他著『方程式の解き方』東京図書1993年
2、北村泰一著『数論入門』槇書店1986年
3、石谷茂著『現代数学と大学入試 Ⅱ』現代数学社1972年
Mathematicaの出力結果だけをいきなりコメントするなんてサイテーです。
↓ポチッと応援お願いします!




























背景に「整数の集合Zに無理数√7を添加した集合」があるというのを
ここで初めて知りました。このようなからくりがあったとは。
この記事を書くために3冊を読み比べました。主に参考にしたのは文献3です。
ペル方程式の向こうには「2次体の整数論」がいます。数論は奥が深いですね。