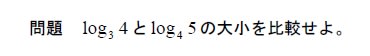
これが出題されたのは数年前の群馬高専の定期試験であったが、大変出来が悪かったと聞いた。それでその解説が私に回って来たのである。

底の変換公式を覚えていて、関数電卓があれば答えは出ますが、これもルール違反です。出題者の意図は対数の定義を理解しているか、にあると思われます。これさえ理解していれば簡単な問題です。

対数の発明は当時の天文学者の寿命を延ばしたと言われるほど画期的であったけれど、現在では数値計算の役割はとっくに終わり、教科書の中にしか生きていない。上の問題なども当時の人なら見た瞬間に解ける問題に違いない。
ロシアの碩学アーノルドの著作『数理解析のパイオニアたち』(シュプリンガー・フェアラーク東京、1999年)には以下のような恐ろしい式が載っている。
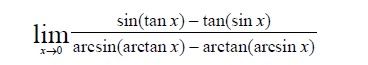
私などは見ただけでげんなりして数式処理ソフトのお世話になってしまうだろう。しかしアーノルドによればバロー、ニュートン、ホイヘンスには数分で解けるらしい。学者の世界でもそうだが、会社も創業者は偉い、ということかな。
↓ポチッと応援お願いします!

(注釈)上の小文は本体のサイトに2004年4月に書いたものです。これを今ブログに掲載するのは本体のサイトをMovableTypeで再構築しているからです。この作業は思ったように進んでいませんが、私の個性が出すぎるものは順次このブログに移行するつもりです。

底の変換公式を覚えていて、関数電卓があれば答えは出ますが、これもルール違反です。出題者の意図は対数の定義を理解しているか、にあると思われます。これさえ理解していれば簡単な問題です。

対数の発明は当時の天文学者の寿命を延ばしたと言われるほど画期的であったけれど、現在では数値計算の役割はとっくに終わり、教科書の中にしか生きていない。上の問題なども当時の人なら見た瞬間に解ける問題に違いない。
ロシアの碩学アーノルドの著作『数理解析のパイオニアたち』(シュプリンガー・フェアラーク東京、1999年)には以下のような恐ろしい式が載っている。
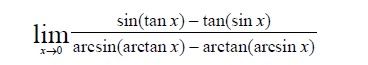
私などは見ただけでげんなりして数式処理ソフトのお世話になってしまうだろう。しかしアーノルドによればバロー、ニュートン、ホイヘンスには数分で解けるらしい。学者の世界でもそうだが、会社も創業者は偉い、ということかな。
↓ポチッと応援お願いします!
(注釈)上の小文は本体のサイトに2004年4月に書いたものです。これを今ブログに掲載するのは本体のサイトをMovableTypeで再構築しているからです。この作業は思ったように進んでいませんが、私の個性が出すぎるものは順次このブログに移行するつもりです。

























>勉強になったのは数式を含むコメントを無料の掲示板を使って行うという 倫理規範に反する ロハ 技 のみ...
他人の母屋を の検索結果 約 17,100 件
他人の母屋を借り;
http://b5.spline.tv/mynb5/?command=GRPVIEW&num=68
早めに返信したいと思ったのですが、昨日も高専ロボコンを観戦したりで一日遊んでしまいました。
Logさんのコメントで勉強になったのは数式を含むコメントを無料の掲示板を使って行うという裏技です。これは全く私には思いつかない手法でした。
しかし、Mathematicaに頼る手法は感心しません。これは私以外のこの記事を読んだ皆さんも同様な感想をお持ちになったと想像します。単調減少を証明するためにx=3とおいて、微分した結果は自然対数で表せます。出てきた式の分子<0であることは、少なくとも高校2年生にとっては自明ではありません。
三角関数と逆三角関数を含んだ極限値の計算も数式処理ソフトで1であることは分かっていました。これをベキ級数に展開してグラフを描くなんてことはMathematicaでは朝飯前でしょう。でもこれはアーノルドさんがあの文章で言いたかったこのと対極を目指すことです。邦訳のP122のノート(図37)にこの計算を図示しています。
ニュートンの『自然哲学の数学的原理』をお読みなれば直ぐに分かりますが、皆が知っていても誰も読まないこの本には数式が一つも出てきません。あるのは私たちに馴染みのない円錐曲線についての「絵」です。彼はあらゆることを図解して理解していたのだと思わざるを得ませんでした。だからあのような極限値の計算も直ぐに幾何学的な意味を察知することが出来るはずだ、と思ったのです。
フランス語は学生時代に2年間ラジオ講座で独学し、それから選択の仏書購読を受講しました。教官は金子光晴の息子さんで、母親(森三千代)の姓を名乗っていました。学生は全部で5名、内3名は暁星出身者で中学から仏語をやっていたやつらです。確かベケットの小説がテキストだったのです。でも仏語はものになりませんでした。今では忘却のかなたにあります。
仏語がお得意なLogさんにお勧めするのはヴォルテールの『哲学書簡』と『カンディード』です。「何はともあれ、我々は我々の畑を耕さなければなりません。」これが小説『カンディード』の結びの言葉です。私もヴォルテールについて記事を書きたくなりました。
(シュプリンガー・フェアラーク東京、1999年)には
以下のような恐ろしい式が載っている。
http://b5.spline.tv/mynb5/?command=GRPVIEW&num=63
と
【畏怖】の念に打たれる feel awed / 《文》be stricken with awe
【畏敬】の念に打たれる be struck with awe
た 所以 を 是非 激白して ください お願い致します。
(その所以が理由不明の儘なら夜も眠れませぬ)
>Mathematicaの使い方はどうしても「力ずく」のように見えます。
>nに小さな数を加えた問題はPC無では出来っこない問題で、美しくないのです。従ってやる気が起こらないのです。
少し誤解されておられます。Mathematicaのお世話になりましたが
略 手で やるのと 同じです;
http://b5.spline.tv/mynb5/?command=GRPVIEW&num=61
(<---もっと違ったアプローチを期待しいた。とは????)
なる単調減少函数から、nに小さな数を加えた問題も瞬時に大小判明なのです。
Mathematicaの使い方はどうしても「力ずく」のように見えます。もっと違ったアプローチを期待していました。
nに小さな数を加えた問題はPC無では出来っこない問題で、美しくないのです。従ってやる気が起こらないのです。
常用対数の値を2~9まで暗算で求める記事を「同じ本を2冊持っている(その3-1)」と題して2007-04-13に書いています。32ビットのIPアドレスの総数を暗算で求める裏技もあります。お読み頂ければ幸いです。
nを底とするn+1の対数をLog(n,n+1)として表現する時、nが大きくなるとLog(n,n+1)は限りなく1に近づく、これがLogさんのいう「単調減少」の別の言い方ですね。群馬高専の問題はこの特別な場合です。
でもね。見たとたんにMathematicaの出力だと分かりました。どうせMathematicaを使うならシンボリックに解けないでしょうか?
有名な「4色問題」の解決はコンピュータを使わない初等的な解決がなされていないのでしょうか?
やはり数学=技芸という考えには違和感を感じます。HAL.Tさんにはいつもお世話になっているので、感情で書くのは失礼だろう、と思いました。
それでこのことについて記事にすべく本を読んで考えています。ただ今仕込み中ですね。
Out[96]=
{Log[3]/Log[2] - Log[4]/Log[3],
Log[4]/Log[3] - Log[5]/Log[4],
Log[5]/Log[4] - Log[6]/Log[5],
Log[6]/Log[5] - Log[7]/Log[6],
Log[7]/Log[6] - Log[8]/Log[7],
Log[8]/Log[7] - Log[9]/Log[8],
Log[9]/Log[8] - Log[10]/Log[9],
Log[10]/Log[9] - Log[11]/Log[10],
Log[11]/Log[10] - Log[12]/Log[11],
Log[12]/Log[11] - Log[13]/Log[12],
Log[13]/Log[12] - Log[14]/Log[13],
Log[14]/Log[13] - Log[15]/Log[14],
Log[15]/Log[14] - Log[16]/Log[15],
Log[16]/Log[15] - Log[17]/Log[16],
Log[17]/Log[16] - Log[18]/Log[17],
Log[18]/Log[17] - Log[19]/Log[18],
Log[19]/Log[18] - Log[20]/Log[19],
Log[20]/Log[19] - Log[21]/Log[20]}
Out[97]=
{0.3231029935782417, 0.10089545969923353,
0.047681294884302616,
0.02724962005768683, 0.01741157117762504,
0.011979894176628925,
0.008690030002745264,
0.006558951986467498,
0.005106122531123081,
0.004075007444388934,
0.003318987796094186,
0.0027495690088570335,
0.002310899138499911,
0.0019663889266769985,
0.00169129811737867,
0.0014684373936704187,
0.0012855783353566963,
0.0011338395531508283}
n--->Log[n, n + 1]は単調減少函数。
溶接をするにあたって、素材に応じた溶接素材を選ぶでしょ。それは溶接技術の一つでしょうしね。そんな意味合いで、数学者にとっても数学は技芸に属すると思うのだ。それを無視して数学者はすべての女王だとか抜かすけれど、裸の女王だね。この女王、若ければ裸の女王がいいけどね。
別に数学者をこの見解で納得させようとは思わないけれど、現実的に見て自分の世界を他の世界の上位構造に位置づけるなんて権威的な数学者の癖じゃないかと思う。
数学や科学史的な分析をいっぱい書き残しているファインマンやノーバートウィーナーなどは数学と技術の手法について、先の見解と同じように捉えている(コマゴマとした知見が基礎になる、ってように見える)。日本の権威ある数学者の見解とは異なるが、彼らのほうが私にあうってだけの事なのかもしれないな。
もっとも、高専の問題、考えてみればそのようなコマゴマとした知見を入試で要求するってこと自体、技芸であることの証明だとも思える。
数学者の自己言及の破綻だろうかな。
この問題は言い直すと「4は3進法の世界は何桁か?5は4進法の世界では何桁か?桁数の大きいのはどっち?」ということです。対数を発明した人にとっては当たり前のことなのですが、Logという記号の操作だけを知る学生には難問なのです。
HALさんの意見にまともに答えようとすると記事10本位になりそうですが、2007年5月30日に書いた「同じ本を2冊持っている(その4)」をちょっと引用します。
「数学は科学者とエンジニアにとっては道具であり、数学者にとっては宗教であるが、一般の人にとっては邪魔者と考えられている。」
ゴードンさんの言う道具がHALさんの言う技芸なんでしょうね。数学と宗教の距離は案外近いかもしれない。
それも私が物理や電気を化学としてみるときは非常に少数の概念ですむのに対して、物理や電気を実現するときには、実現可能性を導くこまごまとして知識がベースになっているからだろう。
そういう意味で、数学を科学としてみるならば、仮説から証明にいたる手法だけは科学。そして、こまごまとした実現手法が技芸に属するものだとしても、私自身の理解構造に違和感はでてこない。
対数の運用も、すこしまえまではこまかな技芸的な知識であったろうと思うので、数学の問題としてはいいだろう。しかし、現代では別の解法を知って実現できるのならばそれはそれでいいんだろうな。
丸善の対数表をいじくる時代は遠くに過ぎ去ったってことだろう。近代の科学が200年の歴史を持つとして、この20年ってのは10%にあたる、それぐらいの変遷があっても当然だと思う。ただし、教育する先生たちは科学と技術の関係について全く認識していないようだね。技術とは科学内部での実現手段でもあるのになあ。