内積について

mixi の話題になっていること。
ベクトルの内積について
そこで、高校生に内積を教えるならどう教えるかみなさんの意見を聞かせてください！

＜私の意見＞
a = (p, q)、b = (s, t)、a、b のなす角をθとすると

a・b ≡ ps + qt と定義する。
a・a = p² + q² = |a|² より a・a = |a|²
a・b = ps + qt = sp + tq = b・a より a・b = b・a が成り立つ。

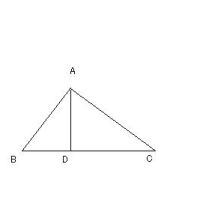
c = b - a と置くと
c = (s - p, t - q) より
c・c = |c|² = (s - p)² + (t - q)² = (s² - 2sp + p²) + (t² - 2tq + q²)
= (s² + t²) - 2(sp + tq) + (p² + q²) = |b|² - 2b・a + |a|²
= |a|² - 2a・b + |b|²　（∵ a・b = b・a）
よって　|c|² = |b - a|² = |a|² - 2a・b + |b|² が成り立つ。

余弦定理より
|b - a|² = |a|² + |b|² - 2|a||b|・cosθ
⇔ |b|² - 2a・b + |a|² = |a|² + |b|² - 2|a||b|・cosθ
⇔ a・b = |a||b|cosθ
よって、a・b = ps + qt = |a||b|cosθ

あなたなら、どのように教えますか？