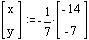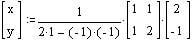多項式の計算

===== 中３ =====
（分配法則）
a(b + c) = ab + ac
(a + b)c = ac + bc

（多項式の公式）
X = c + d とおくと
(a + b)(c + d) = (a + b)X = aX + bX = a(c + d) + b(c + d) = ac + ad + bc + bd
よって、
(a + b)(c + d) = ac + ad + bc + bd　・・・①

①の公式を使用すると
(x + a)(x + b) = x² + bx + ax + ab = x² + (b + a)x + ab = x² + (a + b)x + ab
よって、
(x + a)(x + b) = x² + (a + b)x + ab　・・・②

②の公式を使用すると
(x + a)² = (x + a)(x + a) = x² + (a + a)x + a² = x² + 2ax + a²
よって
(x + a)² = x² + 2ax + a²　・・・③

③の公式を使用すると a を -a とおく
(x - a)² = (x + (-a))² = x² + 2(-a)x + (-a)² = x² - 2ax + a²
よって
(x - a)² = x² - 2ax + a²　・・・④

②の公式を使用すると
(x + a)(x - a) = x² + (a - a)x + a(-a) = x² - a²
よって
(x + a)(x - a) = x² - a²　・・・⑤

（展開の公式）
(a + b)(c + d) = ac + ad + bc + bd
(x + a)(x + b) = x² + (a + b)x + ab
(x + a)² = x² + 2ax + a²
(x - a)² = x² - 2ax + a²
(x + a)(x - a) = x² - a²

（因数分解の公式）
ac + ad + bc + bd = (a + b)(c + d)
x² + (a + b)x + ab = (x + a)(x + b)
x² + 2ax + a² = (x + a)²
x² - 2ax + a² = (x - a)²
x² - a² = (x + a)(x - a)


※高校で習う公式
(x + a)(x + b)(x + c) = x³ + (a + b + c)x² + (ab + bc + ca)x + abc
(x + a)³ = x³ + 3ax² + 3a²x + a³

n! = n(n - 1)(n - 2)・・・3・2・1
1! = 0! = 1 とする
_nC_r = n! / (r!(n - r)!)
例：₅C₃ = 5! / (3!(5 - 3)!) = 5! / (3!2!) = (5・4・3・2・1) / (3・2・1)(2・1) = (5・4) / (2・1) = 5・2 = 10

(x + a)ⁿ = _nC₀xⁿ + _nC₁ax^{n - 1} + _nC₂a²x^{n - 2} + ・・・ + _nC_ra^rx^{n - r} + ・・・ + _nC_{n - 1}a^{n - 1}x + _nC_naⁿ

＜例＞
(x + a)⁵
= ₅C₀x⁵ + ₅C₁ax^{5 - 1} + ₅C₂a²x^{5 - 2} + ₅C₃a³x^{5 - 3} + ₅C_{5 - 1}a^{5 - 1}x + ₅C₅a⁵
= ₅C₀x⁵ + ₅C₁ax⁴ + ₅C₂a²x³ + ₅C₃a³x² + ₅C₄a⁴x + ₅C₅a⁵
= (5! / (0!5!))x⁵ + (5! / (1!(5 - 1)!))ax⁴ + (5! / (2!(5 - 2)!))a²x³ + (5! / (3!(5 - 3)!))a³x² + (5! / (4!(5 - 4)!))a⁴x + (5! / (5!(5 - 5)!))a⁵
= (5! / (0!5!))x⁵ + (5! / (1!4!))ax⁴ + (5! / (2!3!))a²x³ + (5! / (3!2!))a³x² + (5! / (4!1!))a⁴x + (5! / (5!0!))a⁵
※1! = 0! = 1 or 5! / 5! = 1より
= x⁵ + ((5・4・3・2・1) / (4・3・2・1))ax⁴ + ((5・4・3・2・1) / (2・1)(3・2・1))a²x³ + ((5・4・3・2・1) / (3・2・1)(2・1))a³x² + ((5・4・3・2・1) / (4・3・2・1))a⁴x + a⁵
= x⁵ + 5ax⁴ + ((5・4) / (2・1))a²x³ + ((5・4) / (2・1))a³x² + 5a⁴x + a⁵
= x⁵ + 5ax⁴ + 10a²x³ + 10a³x² + 5a⁴x + a⁵

確率

===== 中２ =====
（場合の数）
・場合の数
あることがらの起こり方が全部で n 通りあるとき、n を、そのことがらの起こる場合の数という。

（確率）
・確率
あることがらの起こることが期待される程度を表す数をそのことがらの起こる確率という。
※確率 p ならば　0 ≦ p ≦ 1 である。

・確率の求め方
起こる場合が全部で n 通りあり、それのどれが起こることも同様に確からしいとする。
そのうち、ことがら A の起こる場合が a 通りであるとき、A の起こる確率 p は、次の通りである。
p = a / n


※高校でも、大学でも確率は習います。
大学入試試験でも、確率の問題はよく出題されます。
中学の確率から、覚えるように心がけましょう。

図形の性質

===== 中２ =====
（二等辺三角形）
<<< 定義 >>>
・２つの辺が等しい三角形を二等辺三角形という。

<<< 性質 >>>
・底角は等しい

<<< 条件 >>>
・２角が等しい三角形は、二等辺三角形である。

（直角三角形の合同条件）
・斜辺と他の１辺がそれぞれ等しい
・斜辺と１鋭角がそれぞれ等しい

（円周角の定理）
中心角 = 円周角・2

（平行四辺形）
<<< 定義 >>>
・２組の対辺がそれぞれ平行な四角形を平行四辺形という。

<<< 性質 >>>
・２組の対辺は、それぞれ等しい
・２組の対角は、それぞれ等しい
・対角線はおのおのの中点で交わる

<<< 条件 >>>
・２組の対辺が、それぞれ平行である。
・２組の対辺が、それぞれ等しい。
・２組の対角が、それぞれ等しい。
・対角線がおのおのの中点で交わる。
・１組の対辺が平行で長さが等しい（四角形）。

（特別な平行四辺形）
・長方形　４つの角（90°）が等しい四角形。
・ひし形　４つの辺が等しい四角形。
・正方形　４つの角（90°）が等しく、４つの辺が等しい四角形

図形の調べ方

===== 中２ =====
（対頂角と同位角と錯角）
・対頂角
２つの直線が交わったときにできる、向い合う角を対頂角という。

・同位角と錯角は、言葉で説明が出来ないので、割愛します。
教科書で確認してください。

（平行線と角）
・平行線の性質
２つの平行線の同位角と錯角は等しい

・平行線になる条件
同位角と錯角が等しいならば、２つの線は、平行線である

（三角形の角）
・内角の和は180°である。
・外角 = 内角の２つの和

（多角形の内角と外角）
n角形について
・内角の和 = 180°・(n - 2) (n ≧ 3)
・外角の和 = 360°

（三角形の合同条件）
・３辺が等しい
・２辺とその間の角が等しい
・１辺とその両端の角が等しい

１次関数

===== 中２ =====
x の値が決まると、y の値が決まるとき、y は x の関数である。
※厳密には、f:x → y の写像を考えるとき、y = f(x)と定める。　中学の範囲外なので、覚える必要はありません。

（１次関数の一般形）
y = ax + b
※正確には、ax + by = c が一般形です。

（変化率）
変化の割合 = yの増加量 / xの増加量 = a

（傾きと切片）
y = ax + b のとき
傾きは a
切片は b

（連立方程式とグラフ）
ax + by = c ・・・①
dx + ey = f ・・・②
連立方程式の解と（①と②）のグラフの交点は、一致します。

連立方程式

===== 中２ =====
中２で行う連立方程式は、正式には「２元１次方程式」と言います。
※大学１年の時に線形代数学より「n元１次方程式」を習います。

（加減法）
①・・・x + 2y = 4
②・・・3x - y = 5

①、②×2より
・x + 2y = 4 ・・・①
・6x -2y = 10・・・②'

① + ②' よりyを消去する
7x = 14 ⇒ x = 2

①に代入
2 + 2y = 4 ⇒ 2y = 2 ⇒ y = 1

よって、(x, y) = (2, 1)

（代入法）
①・・・2x - y = 2
②・・・y = x - 1

②を①に代入してyを消去する
2x - (x - 1) = 2 ⇒ 2x - x + 1 = 2 ⇒ x = 1

②に代入する
y = 1 - 1 = 0

よって、(x, y) = (1, 0)

※高校C・Ⅲでは行列を習います。
行列を習うと簡単に解けます。

（一般式）
Ax = b




・逆行列
ad - bc ≠ 0

A^-1


（一般解）
ad - bc ≠ 0

x = A^-1b




（加減法の問題を解く）










（代入法の問題を解く）








中学生が行列を使用して解くことは、範囲外なので、答案で解くことは出来ません。
ただ、穴埋め問題ならば、解いても差し支えありませんが、正確に理解していないので、おすすめは出来ません。

こんな、方法で解く方法があるのだなぁと思って頂ければいいです。

式の加減乗除

===== 中２ =====
（多項式と単項式と次数）
単項式：2、3a、4x³
多項式：3x³ - 2x² - 5x + 7

===== 次数 =====
4a²b² - 3a³ + 4b² - 5a + 7
文字の指定がない場合：４次式（a²b² ⇒ 2 + 2 = 4）

aの次数：３次式（a³）
-3a³ + (4b²)a² - 5a + (4b² + 7)
bの部分は定数と扱う

bの次数：２次式(b²）
(4a² + 4)b² + (- 3a³ - 5a + 7) = 4(a² + 1)b² + (- 3a³ - 5a + 7)
aの部分は定数と扱う

（同類項）
5x² + 3x + 4y - 3x² + 5x - y
同類項：（5x²、3x²）、（-3x、5x）、（4y、-y）
※次数が同じ、文字も同じ場合に、同類項と言う。
※次数が異なる場合と文字が異なる場合は、同類項とは言わない。

（式の加減）
5x² + 3x + 4y - 3x² + 5x - y
= 5x² - 3x² + 3x + 5x + 4y - y
= (5 - 3)x² + (3 + 5)x + (4 - 1)y （※暗算出来るならば省略は可能）
= 2x² + 8x + 3y

（式の乗徐）
3x³y²・4x ÷ 2y = 3x³y²・4x / 2y = 12x⁴y² / 2y = 6x⁴y

空間図形

===== 中１ =====
角柱（T：底面積、h：高さ、S：表面積、V：体積）
S = 側面積 + 底面積・2
V = Th

円柱（r：半径、h：高さ、S：表面積、V：体積）
S = 2πrh + 2πr²
V = πr²h

角錐（T：底面積、h：高さ、S：表面積、V：体積）
S = 側面積 + 底面積
V = Sh / 3

円錐（r：半径、l：母線、中心角：x°、h：高さ、S：表面積、V：体積）
S = 2πl・x°/ 360 = 2πr
V = πr²h / 3

平面図形

===== 中１ =====
（用語の確認）
<<< 直線 >>>
・直線ABは、左右は無限に伸びているイメージ
・線分ABは、長さが決まっていること（左右が有限）
・半直線ABは、右（または左）のみが無限に伸びているイメージ

∠ABC は点Bから線分BAと線分BCの間の角のこと。
垂直は、直線ABと直線CDが垂直を「AB⊥CD」と表す。　角度が90°
平行は、直線ABと直線CDが平行を「AB//CD」と表す。

<<< 円 >>>
孤、弦、中心角、おうぎ形の用語を確認しましょう。

半径r, 円周l, 面積S, 中心角x°とすると
・円の公式
円周 l = 2πr
面積 S = πr²

・おうぎ形の公式
円周 l = 2πr・x / 360
面積 S = πr²・x / 360

<<< 対称 >>>
線対称：ある線を対称にすると同じ図形をする意味
点対称：180°を回転すると同じ図形をする意味

比例と反比例

===== 中１ =====

（比例）
y = 2x の場合
.....
(y, x) = (-4, -2)
(y, x) = (-2, -1)
(y, x) = (0, 0)
(y, x) = (2, 1)
(y, x) = (4, 2)
.....

y = ax の場合
.....
(y, x) = (-2a, -2)
(y, x) = (-a, -1)
(y, x) = (0, 0)
(y, x) = (a, 1)
(y, x) = (2a, 2)
.....

（反比例）
y = 2 / x
.....
(y, x) = (-1, -2)
(y, x) = (-2, -1)
(y, x) = (0, 0)
(y, x) = (1, 1)
(y, x) = (1, 2)
.....

y = a / x (x ≠ 0)
.....
(y, x) = (-a / 2, -2)
(y, x) = (-a, -1)
.....
(y, x) = (a, 1)
(y, x) = (a / 2, 2)
.....

<<< 一般形 >>>
比例：y = ax
反比例：y = a / x

<<< 抽象化 >>>
中学のレベルは、超える内容です。
なので、こんな風に考えるのだなあと感じて頂ければいいです。
x の値が決まれば、y の値が決まります。
これを、関数と言います。
f: x → y または y = f(x) と書きます。
この２つの書き方は、厳密には意味合いが少し異なる部分がありますが、現段階では、気にする必要はないと思います。

<<< 参考までに >>>
一応は、違いを書きますけど、現段階では覚える必要はありません。
f: x → y は、集合論での写像を表す書き方です。
y = f(x) は、解析学の関数を表す書き方です。
今回の比例、反比例は、関数の１部ととらえることが、普通なので、y = f(x) と書き表すことが一般的です。

厳密には、f: x → y の特殊な場合が、y = f(x)と考えます。
高校で習いますけど、x = 行列A, f = 行列M とすると y = MA = 行列B と表すことも出来ます。　この場合も、f: x → y とも表せます。