統計のコツのこつ(10)

このブログは「すぐに役立つ統計のコツ」(オーム社)の副教材の様なものです。
今回は、本書で紹介できなかった「カイ二乗検定」の計算方法です。

 

それでは、「すぐに役立つ統計のコツ」第５章(40ページ)を開いて下さい。

 

本書の例題(データ)は下記の情報統計研究所(HP)からダウンロード出来ますのでご利用下さい。

 

 

医学や看護関連の分野では、実験やアンケート集計などの出現度数（出現頻度）を分割表形式（クロス集計）にまとめる事がよくあります。
例えば、本章の「表5.1」(40ページ)の様にです。

 

***
表5.1を次のように訂正します。
非正規（病気なし）→非生起（病気なし）

 

「すぐに役立つ統計のコツ」の正誤表は下記に記しています。
正誤表←ここをクリック
***

 

この様な表を一般に「２×２分割表」と言い、２行Ｌ列やＭ行Ｌ列にまとめる事もあります。

 ここで、

「２×２分割表」が与えられたとき、一般には「カイ二乗検定」の対象となります。
その１例を本章の「表5.5」について次の様にまとめてみましょう。

 

表5.5　性別とコレステロール値の分割表
 

 

 

与えられた度数をもとに、
行の度数の比率(%)と列の度数の比率(%)そして全体の度数の比率(%)を求めて観察します。
そして、比率に差があるかどうかであれば、次により統計的な検定を行います。

 

検定の計算は次の手順で行えば良いでしょう。

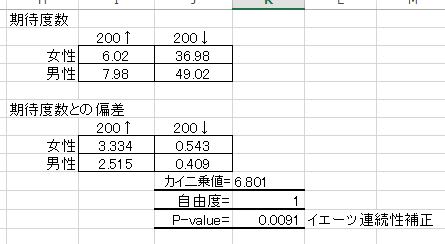
１）期待度数を求める。
Ａ×Ｄ／Ｔ＝４３×１４／１００＝6.02
Ａ×Ｅ／Ｔ＝４３×８６／１００＝36.98
Ｂ×Ｄ／Ｔ＝５７×１４／１００＝7.98
Ｂ×Ｅ／Ｔ＝５７×８６／１００＝49.02

 

２）出現度数と期待度数の偏差（イエーツの補正）
(11－6.02－0.5)^2／6.02＝3.334
(32－36.98＋0.5)^2／36.98＝0.543
(3－7.98＋0.5)^2／7.98＝2.515
(54－49.02－0.5)^2／49.02＝0.409

 

ここで、
「イエーツの補正」は「±0.5」によって行います。

 

３）検定統計量を求める。
カイ二乗値＝出現度数と期待度数の偏差の合計＝6.801

 

4)ｐ値を求める。
Excel関数（CHIDIST）を用いると良いでしょう。
　CHIDIST(6.801, 1)＝0.0091

 

 

 

以上は、期待度数からの計算でしたが「２×２分割表」の場合は、次の別法を
用いても良いでしょう。

 

カイ二乗検定の別報

１）計算（１）
　100×(abs(11×54－32×3)－100／2)^2＝20070400 

２）計算（２）
　(43×57×14×86)＝2951004

 ３）カイ二乗値
　計算(1)／計算(2)＝20070400／2951004＝6.801

４）ｐ値
　Excel関数（CHIDIST）を用いると良いでしょう。
　CHIDIST(6.801, 1)＝0.0091

 

***
本章のExcelによるオッズ比(Odd ratio)の計算（47ページ）に誤りがありますので、次の様に訂正します。

　OR＝（ａ/ｃ）／（ｂ/ｄ） 

***

「すぐに役立つ統計のコツ」の正誤表は下記に記しています。
正誤表←ここをクリック

 

次回は、
引き続き「すぐに役立つ統計のコツ」から第５章についてご紹介します。

 

 

 

情報統計研究はここから