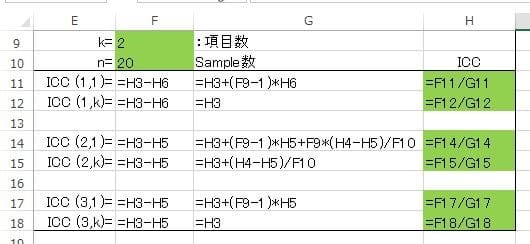
ルーチンに追われていましたが、チョット暇ができましたので先の血清CPK活性値の2元配置分散分析を"SPSS"でやってみました。
「統計のコツのこつ(48)(49)」では、採血した血清を室温と冷所に1時間と2時間放置したときのCPK活性値の変化を見たものでした。統計的検討では"差の検定"や"2元配置分散分析"の対象となります。
ここでは、
SPSSによる2元配置分散分析の方法をご紹介しましょう。
SPSSによる2元配置分散分析の方法をご紹介しましょう。
SPSSを立ち上げ、図1の様な縦長のデータ形式にします。
図1 縦長形式にしたデータ

sample(名義尺度)=検体番号、time(名義尺度)=1時間放置(1):2時間放置(2)、diff=冷所保存と室温保存の差
次に、
分析→一般線形モデル→1変量→従属変数[diff]、固定因子[sample,time]→モデル→ユーザの指定による→
モデル[sample(F),time(F)]→項の構築[主効果]→続行→OK
分析→一般線形モデル→1変量→従属変数[diff]、固定因子[sample,time]→モデル→ユーザの指定による→
モデル[sample(F),time(F)]→項の構築[主効果]→続行→OK
これで、
図2の2元配置分散分析表が得られます。
図2の2元配置分散分析表が得られます。
図2 2元配置分散分析表

なお、
SPSSの平方和タイプは"Ⅲ"ですが、"Ⅱ"の商用統計ソフトもあります。今のところ、どちらが良いとは言えないようです。
SPSSの平方和タイプは"Ⅲ"ですが、"Ⅱ"の商用統計ソフトもあります。今のところ、どちらが良いとは言えないようです。
ここで、
図2の分散分析表の解釈は、下記の杉本典夫先生の分析結果(図3)とコメントを参考にして下さい。
図2の分散分析表の解釈は、下記の杉本典夫先生の分析結果(図3)とコメントを参考にして下さい。
図3 杉本典夫先生の分析結果
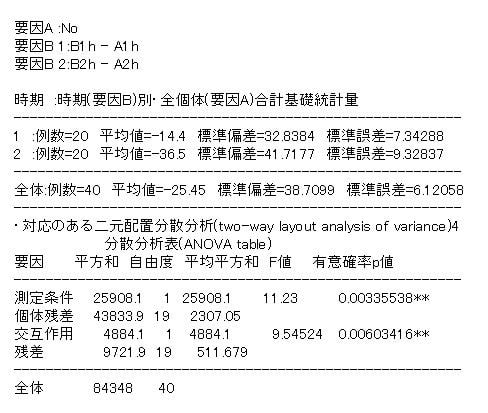

杉本典夫先生の分析結果に対するコメント(原文のまま)
******************
「測定条件」の検定結果は、
1hと2hのデータを平均してAとBで比較したものでありAよりもBの方が平均して-25.45だけ低いことが有意かどうかを検定しています。「交互作用」の検定結果は測定条件(A・B)と測定時間(1h・2h)の交互作用であり1hの平均低下値-14.4と2hの平均値低下値-36.5の差が有意かどうかを検定しています。これらの結果から冷蔵庫保管と比較すると室温保管は低い値になりその低下値は1hよりも2hの方がより大きいことがわかります。この分析結果をより詳細に検討するため、級内相関係数、相関係数、回帰係数を求めるのが本来の手順です。
******************
******************
「測定条件」の検定結果は、
1hと2hのデータを平均してAとBで比較したものでありAよりもBの方が平均して-25.45だけ低いことが有意かどうかを検定しています。「交互作用」の検定結果は測定条件(A・B)と測定時間(1h・2h)の交互作用であり1hの平均低下値-14.4と2hの平均値低下値-36.5の差が有意かどうかを検定しています。これらの結果から冷蔵庫保管と比較すると室温保管は低い値になりその低下値は1hよりも2hの方がより大きいことがわかります。この分析結果をより詳細に検討するため、級内相関係数、相関係数、回帰係数を求めるのが本来の手順です。
******************
なお、
2元配置分散分析については、下記URL(統計学入門)を参考になさって下さい。
http://www.snap-tck.com/room04/c01/stat/stat04/stat0401_2.html
2元配置分散分析については、下記URL(統計学入門)を参考になさって下さい。
http://www.snap-tck.com/room04/c01/stat/stat04/stat0401_2.html
情報統計研究所はここから!