統計技術 第Ⅲ部 Free Online Caluclator (例題集)
第4章:Skewness-Kurtosis Plot(Cullen and Frey graph)
Skewness(歪度) と Kurtosis(尖度) テストについては、既に、「統計技術 第Ⅲ部:第1章-3 Histogram(データの分布)」で紹介した.
https://blog.goo.ne.jp/k-stat/e/b1a12b4c9c3bc356d66b9eefb7476f7c
ここでは、
Wessa.net Topページから、
↓
Statistical Distribution→Skewness-Kurtosis Plot
↓
Data を確認
↓
Compute
出力結果:
図1Empirical density ana Cumlative distribution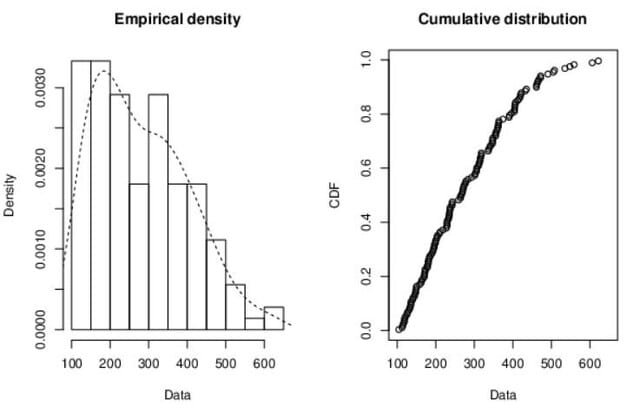
通常のヒストグラムと経験的密度関数を表している.
図2 skewness-kurtosis plot (Cullen and Frey graph)
当てはめの良さを表すプロット(Cullen and Frey graph)は、一般的にピアソン プロットなど、いくつかの名前があり、歪度と尖度の関係を表しており、視覚的に歪んだ分布かどうかを見るために考案された.
図2の SkewnessとKurtosisの値は、下記URLの「統計技術 第Ⅲ部:第1章-3 Histogram(データの分布)」から、Skewness=0.57707、Kustosis=2.60623 であり、これは図2の●点(Skewness^2=0.333)の位置にあり、ブートストラップによるシュミレーションでは黄色の散布点のように灰色部分のbeta分布領域に散布することが視覚的に知ることができる.そして、どの分布が自分のデータに最も適しているかを確認しモデルの構築の参考にすれば良いと思う.









